티스토리 뷰
I. 문제
저항과 캐패시터를 사용하여 충전 및 방전회로를 시뮬레이션 해보았습니다.
아래 회로의 캐패시터의 용량과 저항, 전압의 상관관계를 조사합니다.
II. 실습

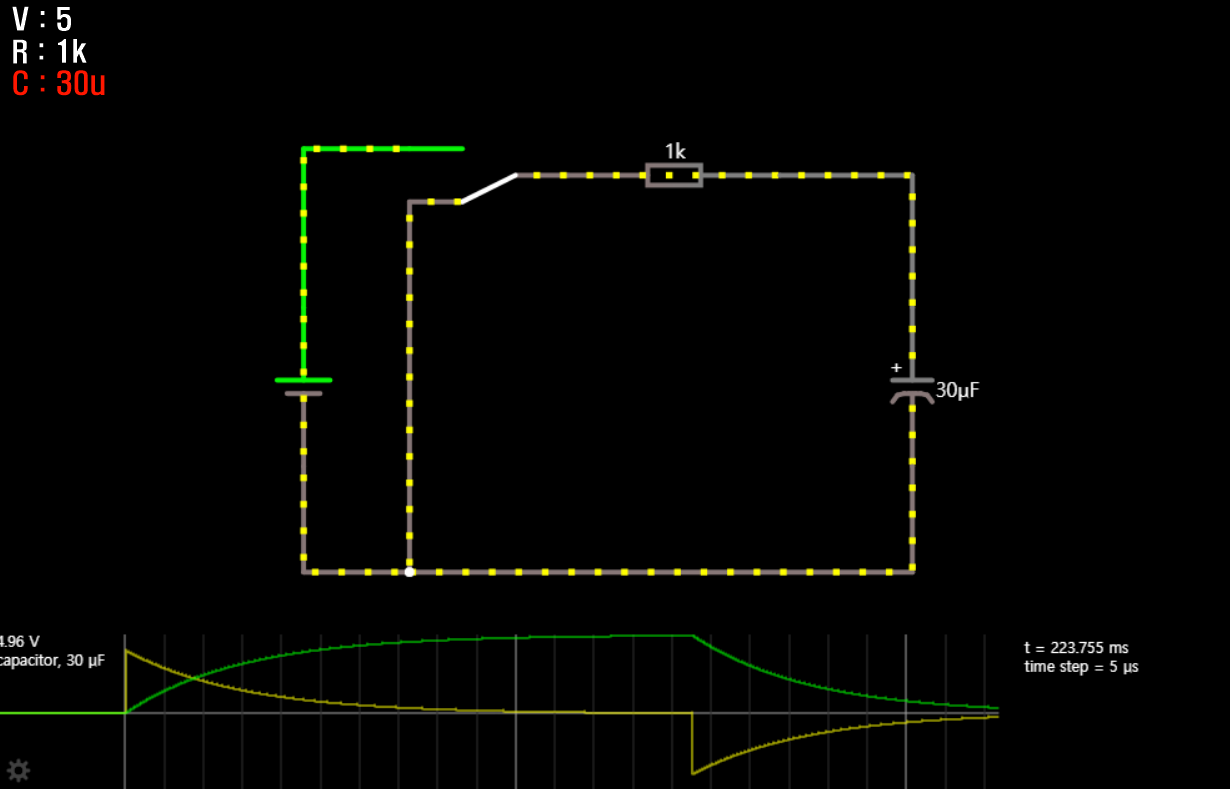
먼저 가장 기본이 되는 회로입니다.
전압의 증감은 모두 지수함수 그래프의 모양을 띄며 그려지는 것을 확인할 수 있었습니다.
저는 이 회로를 기준으로 수치를 변화시키며
캐패시터의 전압변화를 살펴보았습니다.


캐패시터의 용량을 2배, 3배 늘려본후 1번과 비교해 보았습니다.
사진에는 잘 나타나지 않았으나 여러번 실행해본 결과
충전되는 시간도 약 2배, 3배로 늘어난 것을 확인할 수 있었습니다.



다음은 저항을 2k, 4k로 늘려 비교해 보았습니다.
캐패시터의 용량을 늘렸을 때와 같이
약 2배 정도 차이가 나는것을 확인할 수 있었습니다.


전원의 전압을 늘리니 충전이 증가된 만큼 이루어지는 것을 확인할 수 있었습니다.
그렇다면 충전시간에는 차이가 없을까하고 재어보니
6번 7번과 같은 미미한 차이에서는 찾아보기가 힘들고
3V → 약 90s
30V → 약 110s
60V → 약 120s
위와 같이 비교하는 범위가 커져야 차이를 확인할 수 있었습니다.


이번에는 요소 모두를 2배로 증가시켜 보았습니다.
y축이 늘어난 것을 감안 하더라도 모든면에서 꽤 차이가 나는 것을 볼 수 있었습니다.

9번은 전원을 제외한 나머지를 증가시켜보았습니다.
단순하게 4배 정도 차이가 나지 않을까? 했었는데,
1번의 충전시간 : 약96초
9번의 충전시간 : 370~380초
실제로 4배에 꽤 가까운 충전시간을 확인할 수 있었습니다.


10번의 결과는 2번과 ,11번의 결과는 4번과 비슷했습니다.
(둘다 약 7초 차이)
6번 7번과 같이 전원의 전압보다는
캐패시터의 용량과 저항에 더 영향을 받은듯한 결과로 보입니다.
III. 결론
1. 캐패시터의 용량이 늘어나는 만큼 충전, 방전시간이 길어진다.
2. 저항이 커지는 만큼 충전, 방전시간이 길어진다.
3. 전원의 전압을 늘리면 캐패시터의 전압도 커진다.
감사합니다.
공부한 내용을 복습/기록하기 위해 작성한 글이므로 내용에 오류가 있을 수 있습니다.
'Digital Logic' 카테고리의 다른 글
| [기초전자회로] 미·적분 합산회로 시뮬레이션 (0) | 2023.10.31 |
|---|---|
| [기초전자회로] 반전회로/미분회로/적분회로 시뮬레이션 (0) | 2023.10.31 |
| [디지털 논리회로] JK 플립플롭(JK Flip-Flop) 비동기식/동기식 카운터 만들기 (0) | 2023.10.30 |
| [디지털 논리회로] 디코더(Decoder)와 멀티플렉서(MUX) 실습 (0) | 2023.10.30 |
| [디지털 논리회로] 게이트로 5x32 디코더(decoder) 회로도 구현하기 (0) | 2023.10.30 |
