티스토리 뷰
아래글에 이어 작성된 글입니다.
[인공지능] 인공지능과 딥러닝
[인공지능의 의미와 딥러닝] 인공지능이란 무엇이고 10년대 들어 자꾸 언급되는 딥러닝은 무엇일까요? 결론적으로 말하면 인공지능의 하위 집합에 딥러닝이 포함된다고 볼 수 있습니다. 인공지
munak.tistory.com
탐색은 가장 오래된 인공지능 기법입니다. 초기의 AI 프로그램은 여러 탐색 알고리즘을 사용해 문제를 해결하려고 했습니다. 하지만 탐색은 복잡한 문제일수록 기하급수적인 연산량을 요구하게 되고, 그 당시에 그만한 연산을 해낼 CPU의 속도나 충분한 메모리가 개발되지 않았었기 때문에 인공지능은 첫 번째 겨울(암흑기)을 맞게 됩니다.
지금도 딥러닝을 사용해 모델을 학습할 때, 좋은 사양의 컴퓨터로 충분한 시간을 들여 학습해야 유의미한 결과가 나옵니다. 안타깝지만 환경이 갖춰지지 않은 상태에서 간단한 문제만을 해결할 수 있는 초기 인공지능은 외면 받을 수밖에 없었습니다.
이번 글에서는 여러 탐색 알고리즘을 살펴보겠습니다. 탐색은 시작 상태에서 목표 상태까지의 경로를 찾았다면, 문제를 해결했다고 보는 방법입니다. 여기서 말하는 상태란, 특정 시점에 문제가 처한 상황이나 모습을 뜻하고 상태 공간이란, 문제 해결 중 나타나는 여러 상태들의 집합을 의미합니다.
맹목적 탐색
목표 노드의 위치에 관계없이 순서에 따라 상태 공간 그래프를 생성해가며 해를 찾는 방법입니다.
8-puzzle 예시를 들어 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)에 대해 좀 더 살펴보겠습니다. 8-puzzle은 아래와 같이 순서대로 패널을 놓아 푸는 퍼즐입니다. 빈칸이 움직인다고 생각하면 다음 경우의 수는 빈칸이 위, 아래, 오른쪽, 왼쪽으로 움직인다고 할 수 있습니다.

경우의 수에 따라 상태 공간 그래프를 생성하면 다음과 같이 됩니다. 상태를 어떻게 확장한다는 것인지 의미가 이해 되셨다면 다음으로 넘어가 보겠습니다.

깊이 우선 탐색 (Depth-first search)
깊이 우선 탐색은 초기 노드에서 해가 존재할 가능성이 있다면 계속 자식노드를자식 노드를 추가하여 깊이를 우선적으로 탐색하는 방법입니다. 더 이상 자식 노드를 추가할 수 없다면, 부모 노드로 되돌아가(백트래킹) 반복합니다.
위 상태(초기노드에 대해 깊이 우선 탐색 실행)에서 깊이 우선 탐색을 사용해 탐색을 시작하면 다음과 같이 노드가 확장됩니다.

그런데 중복 상태(노란색)가 발생하는 문제가 있습니다. 따라서 후에 알고리즘에서는 OPEN 리스트와 CLOSED 리스트라는 개념을 도입해 중복을 방지합니다. 지금은 이해를 돕기 위해 중복 상태는 제외해 상태 공간 그래프를 그려보겠습니다. 계속해 확장시키면 다음과 같이 됩니다.

가장 왼쪽의 자식을 먼저 확장한다고 할 때 위와 같이 확장이 됩니다. 이렇게 확장한 자식 노드를 우선적으로 탐색해 목표노드에 도달할 때까지 반복합니다. 더 이상 확장할 수 없을 때에는 위에서 언급했다시피 부모로 되돌아가 다른 자식 노드들을 확장해 가며 탐색합니다.

예를 들어 가장 깊은 상태(파란색)의 자식노드들을 모두 확인했음에도 목표 상태에 도달하지 못했다면 부모 노드(초록색)로 되돌아갑니다. 하지만 다른 상태가 없음으로 다시 한번 부모 노드로 되돌아가고 그의 다른 자식인 빨간색 상태에서 다시 탐색을 시작하게 됩니다.
알고리즘은 다음과 같습니다. 잠깐 언급했던 OPEN 리스트와 CLOSED 리스트를 사용하며, 그중 OPEN 리스트를 스택처럼 사용해 가장 깊은 상태를 가져올 수 있도록 구현하면 됩니다.
OPEN 리스트 : 확장은 되었으나 아직 탐색하지 않은 상태들이 들어있는 리스트
CLOSED 리스트 : 탐색이 끝난 상태들이 들어있는 리스트depth_first_search()
{
open <- [시작 노드]
closed <- [ ]
while open =! [ ] do
X <- open 리스트의 첫번재 요소
if X == goal then return SUCCESS
else
X의 자식 노드를 생성한다 (연산자 적용)
X를 closed 리스트에 추가한다
X의 자식 노드가 이미 open이나 closed에 있다면 버린다
남은 자식 노드들은 open의 처음에 추가한다 (스택처럼 사용)
return FAIL
}
너비 우선 탐색 (Breadth-first search)
너비 우선 탐색은 초기 노드에서 인접한 노드들을 우선적으로 방문하는 방법입니다. 인접한 노드들을 우선적으로 둔다는 것이 모호한데, 위와 같이 이 상태(초기 노드에 대해 너비 우선 탐색 실행)에서 너비 우선 탐색을 2번 진행시켜 보겠습니다.

그럼 아래와 같이 됩니다. 차이가 느껴지시나요? 가장 깊은 자식 노드가 기점이 되는 것이 아니라 초기 노드에 가까운, 확장을 한 순서대로 탐색하고 있습니다. 이때 파란색 상태들은 확장은 되었으나 아직 탐색이 되지 않았습니다. 한번 더 진행시켜 보겠습니다.
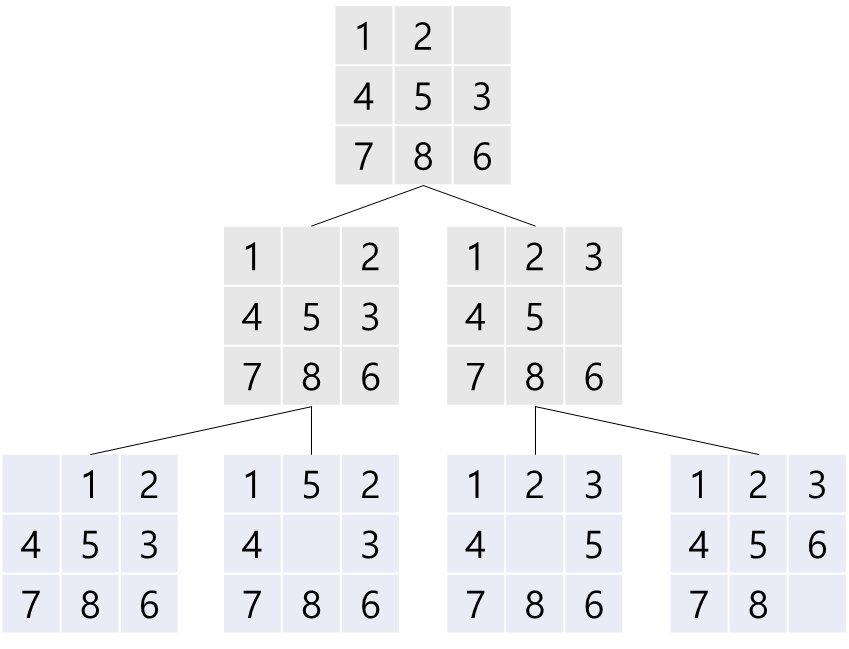
그럼 아래와 같이 되겠네요. 탐색을 성공하면서 탐색이 종료된 모습입니다.

알고리즘은 다음과 같습니다. 이번에는 확장한 순서대로 차례대로 탐색해야 하기에 리스트를 마치 큐처럼 사용하여 구현하면 됩니다.
breadth_first_search()
{
open <- [시작 노드]
closed <- [ ]
while open =! [ ] do
X <- open 리스트의 첫번재 요소
if X == goal then return SUCCESS
else
X의 자식 노드를 생성한다 (연산자 적용)
X를 closed 리스트에 추가한다
X의 자식 노드가 이미 open이나 closed에 있다면 버린다
남은 자식 노드들은 open의 마지막에 추가한다 (큐처럼 사용)
return FAIL
}
경험적인 탐색
다음은 경험적인 탐색입니다. 정보 이용 탐색(Informed search), 휴리스틱 탐색(heuristic search)으로도 불리며 탐색 과정에서 상태 공간에 대해 경험적으로 얻을 수 있는 지식이나, 효율적인 해를 얻을 거란 직관을 기반으로 탐색하여 효율을 높힌 방법입니다. 맹목적인 탐색으로는 해결하기 어려운 문제나 정의하기 힘든 문제를 해결하는 데에 사용합니다. 우리가 어떠한 문제를 해결해 나갈 때 과거에 얻은 지식들을 활용하는 것과 유사한 방법이라고 생각하시면 됩니다.
먼저 휴리스틱에 대해 정의할 필요가 있습니다. 앞서 경험적인 탐색은 경험적 지식이나, 직관을 이용해 탐색을 한다고 했었습니다. 이에 대해 추론하는 것이 휴리스틱입니다. 현재 주어진 상태에서 빠르게 어림짐작해 다음 상태를 선택할 수 있도록 하는 것이죠. 어떤 휴리스틱을 정의하느냐에 따라 탐색결과는 천차만별입니다. 그리고 이 휴리스틱을 넣어 평가하여 점수를 매길 수 있도록 하는 평가함수가 있습니다. 아래는 이를 이용한 여러 기법들 입니다.
언덕 등반 기법(Hill-climbing method)
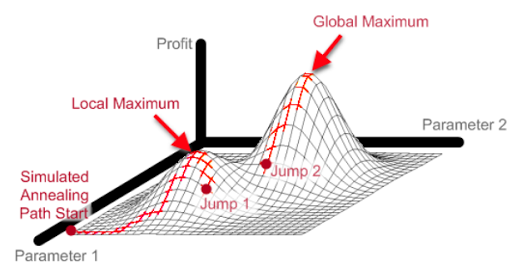
과거의 값은 생각하지 않고 현재 노드에서 확장 가능한 노드들 중에서 휴리스틱에 의한 평가함수 값이 가장 좋은 상태 하나를 선택해 확장하며 탐색하는 방법입니다. 현재 상태를 중심으로 더 이상 좋은 해가 나타지 않으면 반복을 중지합니다. 하지만 이러한 특징 때문에 지역 최대값을 최적의 해라고 잘못 판단할 수 있습니다. 즉 탐색 결과가 항상 최적의 해라는 보장이 없습니다.
[알고리즘]
1. 먼저 현재 위치를 기준으로해서, 각 방향의 높이를 판단한다 (노드의 확장)
2. 만일 모든 위치가 현 위치보다 낮다면 그곳을 정상이라고 판단 (목표 상태인지 검사)
3. 현 위치가 정상이 아니라면 확인된 위치중 가장 높은 곳으로 이동한다 (후계노드의 선택)
A* 알고리즘(A-Star algorithm)
A* 알고리즘은 전체 비용이 최소인 노드를 확장하여 최소 비용 경로를 찾는 방법입니다. 경로 비용을 정확히 계산할 수 없기 때문에 다음과 같이 휴리스틱 평가함수 \( f(x) \)를 정의하여 탐색합니다. 위키백과에서 8-puzzle을 이용한 좋은 예시를 들고 있습니다. 직관적으로 A*알고리즘에 대해 설명하고 있으니 한번 살펴보시는 것을 추천합니다.
\( f(x) = g(x) + h(x) \)
\( g(x) \): 출발로부터 노드 x까지의 경로 가중치
\( h(x) \): 노드 x로부터 목표까지의 추정 경로 가중치
A* 알고리즘 - 위키백과, 우리 모두의 백과사전
정보과학 분야에 있어서, A* 알고리즘(A* algorithm 에이 스타 알고리즘[*])은 주어진 출발 꼭짓점에서부터 목표 꼭짓점까지 가는 최단 경로를 찾아내는(다시 말해 주어진 목표 꼭짓점까지 가는 최단
ko.wikipedia.org
AStar_search( )
{
open <- [시작노드]
closed <- [ ]
while open != [ ] do
X <- open 리스트에서 가장 평가 함수의 값이 좋은 노드
if X == goal then return SUCCESS
else
X의 자식 노드를 생성한다.
X를 closed 리스트에 추가한다.
if X의 자식 노드가 open이나 closed에 있지 않으면
자식 노드의 평가 함수 값 f(n) = g(n) + h(n)을 계산한다.
자식 노드들을 open에 추가한다.
return FAIL
}
게임트리
다음으로 게임을 위한 탐색 알고리즘을 살펴보겠습니다. 먼저 게임에 대한 조건이 있습니다. 두 명의 경기자가 진행하며, 제로썸 게임(한 경지가의 승리는 다른 경기자의 패배)이면서 순차적인 게임(차례대로 수를 두는 게임)이어야합니다.
미니맥스 알고리즘
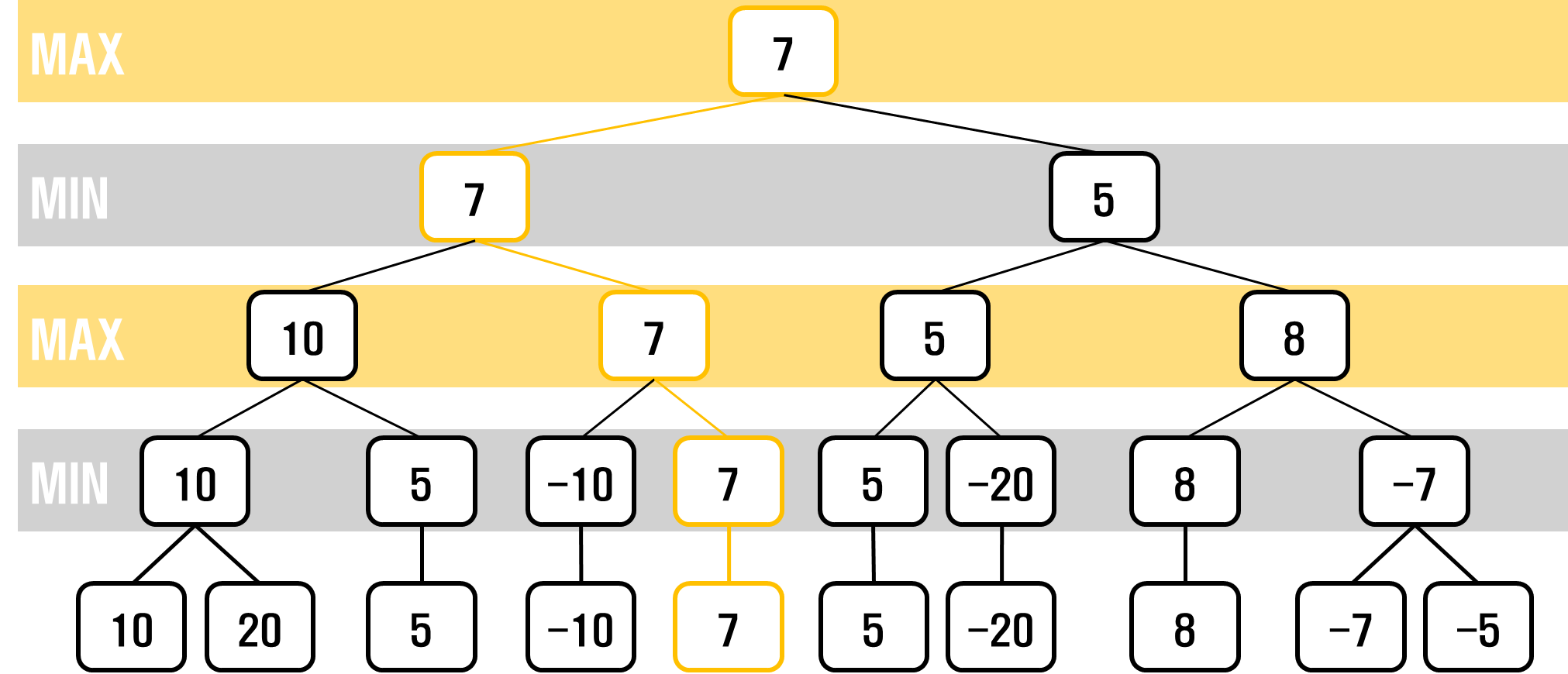
미니맥스 알고리즘은 이런 게임트리에서 자신과 상대방의 상태를 모두 고려해, 노드에 가치를 부여하고 자신의 차례에서는 평가 함수가 최대인 것을, 상대방의 차례에서는 가장 최소를 선택한다고 가정하고 자신에게 가장 유리한 수를 찾을수 있도록 하는 탐색 방법입니다.
function minimax(node, depth, maxPlayer)
{
if depth == 0 or node 가 단말 노드 then
return node의 휴리스틱 값
if maxPlayer then
vaule <- -∞
for each child of node do
value <- max(value, minimax(child, depth -1, FALSE))
return value
else
value <- +∞
for each child of node do
valse <- min(value, minimax(child, depth-1, TRUE))
return value
}
감사합니다.
공부한 내용을 복습/기록하기 위해 작성한 글이므로 내용에 오류가 있을 수 있습니다.
'인공지능' 카테고리의 다른 글
| [인공지능] 다층 퍼셉트론 (MLP)과 역전파 알고리즘 (1) | 2022.08.08 |
|---|---|
| [인공지능] 인공신경망의 시작, 퍼셉트론 (0) | 2022.08.02 |
| [인공지능] 머신러닝과 인공신경망 (feat. 분류, 회귀) (0) | 2022.07.11 |
| [인공지능] 전문가 시스템과 지식 (0) | 2022.01.18 |
| [인공지능] 인공지능과 딥러닝 (0) | 2022.01.10 |
