티스토리 뷰
B-Tree와 B+Tree트리에 대하여
[DB] 인덱스(Index)
데이터 베이스 인덱스에 대하여 인덱스(Index)란? 인덱스는 데이터 베이스 레코드에 빠르게 접근하기 위해서 키와 값(포인터, 주소)의 쌍으로 구성되는 데이터 구조입니다. 데이터베이스를 책이
munak.tistory.com
B+Tree는 리프 노드에만 데이터를 저장하고, 연결 리스트로 구성되어 있기에 범위 검색에 더 효율적입니다.
인덱스 관련한 글에서 B+Tree의 장점을 위와 같이 설명했었습니다.
왜 B-Tree에 비해 B+Tree가 더 범위 검색에 효율적인 걸까요? 이번글에서 정리해보려고 합니다.
B-Tree
B-Tree는 널리 쓰이는 인덱스 자료구조 중 하나입니다.
B-Tree는 이진 트리를 확장한 형태로, 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조입니다.
이진트리의 확장?
이진트리(Binary Tree)는 자식을 최대 2개까지만 가지는 트리를 말합니다.
맨 위의 노드를 루트(root) 노드라고 하고, 각 노드는 왼쪽 자식(left child) 노드와 오른쪽 자식(right child) 노드를 가질 수 있습니다.
그 중에서도 각 노드의 왼쪽 서브트리에는 해당 노드보다 작은 값의 노드들이, 오른쪽 서브트리에는 해당 노드보다 큰 값의 노드들이 위치하도록 정렬한 이진트리를 이진 탐색 트리(Binary Search Tree)라고 합니다.

이진 탐색 트리는 검색, 삽입, 삭제 등의 연산을 평균 O(log n)의 시간 복잡도로 수행할 수 있다는 장점이 있습니다.
즉, 빠른 연산의 장점을 가져오기 위해 인덱스는 이진 탐색 트리 구조를 채택한 것이죠.
근데 왜 이진 탐색 트리를 사용 하지 않고, 노드의 개수를 늘린 새로운 B-Tree 를 만들어 사용하는 걸까요? 🤔
답은 좀 더 균형있고 낮은 트리를 구성할 수 있기 때문입니다.
이진 탐색 트리는 트리가 불균형하게 구성되는 최악의 경우 O(n)의 시간복잡도를 가지게 됩니다.
B-Tree는 노드가 더 많은 값의 범위를 다루기에 이를 완화할 수 있습니다.
따라서 대용량 처리에서도 B-Tree가 좀 더 안정적인 성능을 보여줍니다. 물론 구현은 더 까다로워지겠지만요.
M차 B-Tree
M차 B-Tree 는 최대 M개의 자식을 가질 수 있는 B-트리를 말합니다.
예를 들어 3차 B-Tree 는 최대 아래와 같이 3개의 자식을 가질수 있습니다.
B+Tree
B+Tree는 B-Tree의 변형으로, 데이터베이스에서 널리 사용되는 자료구조 중 하나입니다.
리프 노드에만 데이터를 저장하고, 연결 리스트로 구성되어 있기에 범위 검색에 더 효율적입니다.
B-Tree 는 노드의 key 마다 data를 가졌었죠.
B+Tree 는 리프 노드에만 data를 저장합니다. 리프 노드가 아니라면 자식의 key값을 저장합니다.
리프노드의 부모 key는 리프노드의 첫번째 key보다 작거나 같을 수 있기 때문에 중복되는 key가 발생할 수 있습니다.
또한 리프노드는 연결리스트의 형태 되어있어 인접한 다음 노드에 바로 접근할 수 있습니다.

탐색
탐색 방법은 크게 다르지 않습니다. 아래에서 어떻게 탐색이 이루어지는지 확인해 볼까요?
B-Tree 탐색
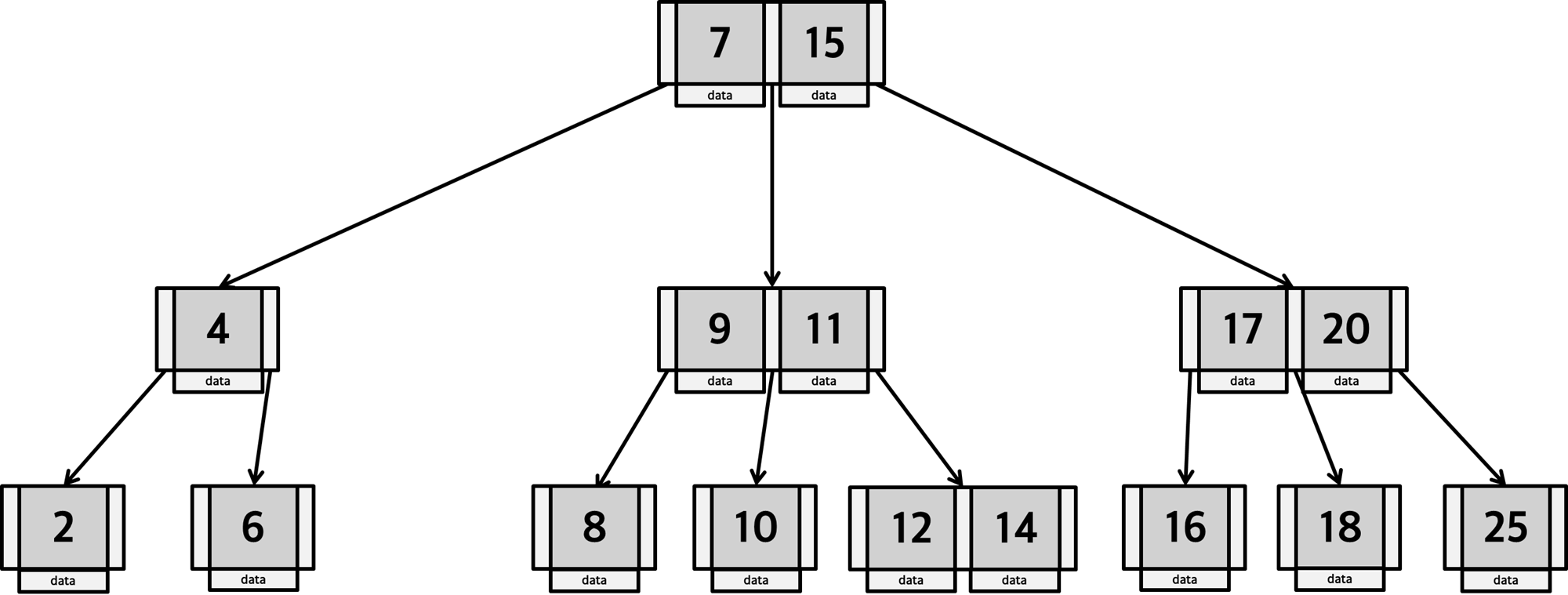
아래 B-Tree 에서 key : 14를 찾는다고 가정해 보겠습니다.

1. 루트 노드의 키값을 순서대로 확인합니다.
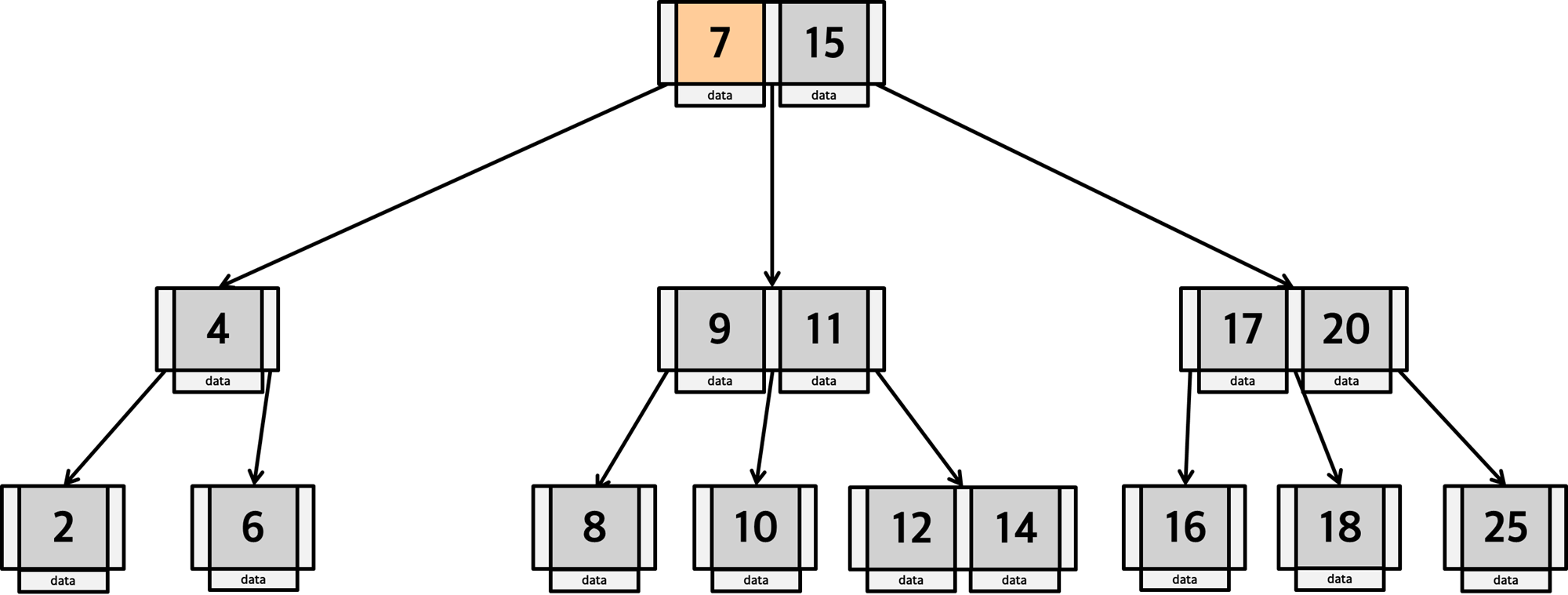
2. 14는 7보다 크므로 다음 key를 확인. 15보다는 작으므로 사이에 있는 포인터가 가리키는 자식노드로 이동합니다.
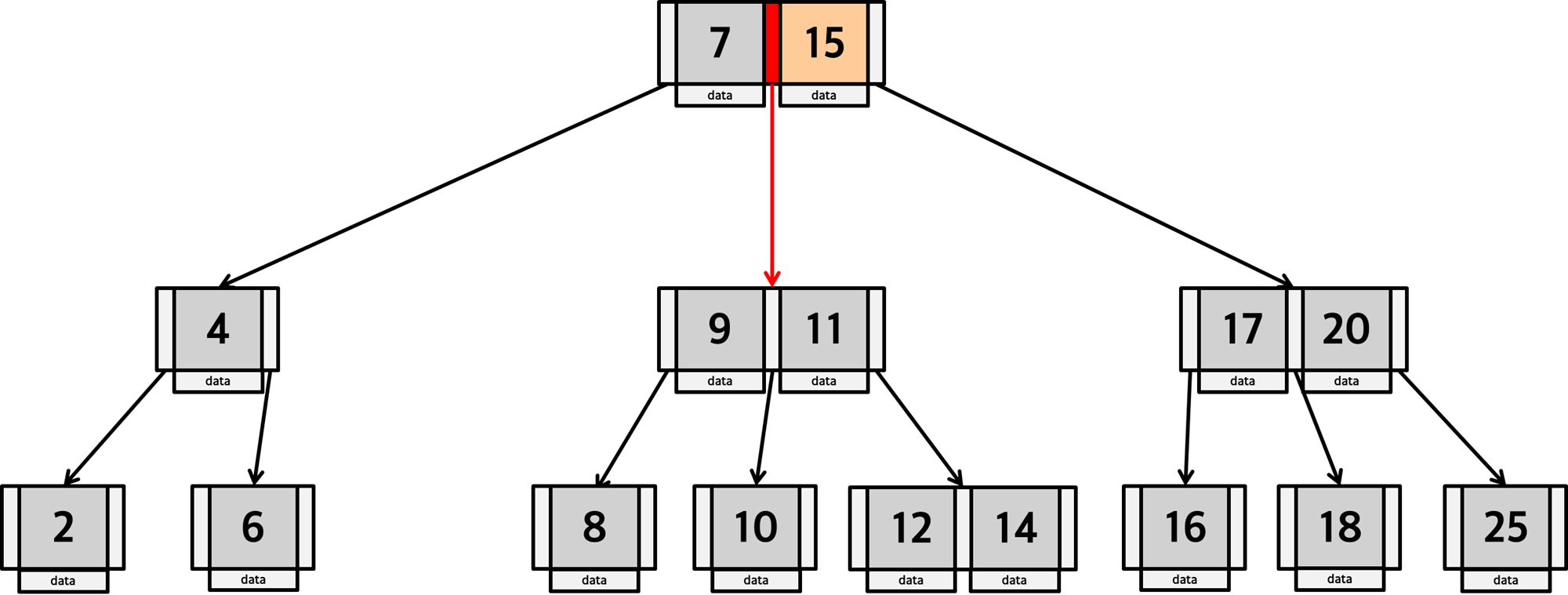
3. 자식으로 이동한 후 다시 순서대로 key를 확인합니다. 9보다 크므로 다음 key를 확인합니다.
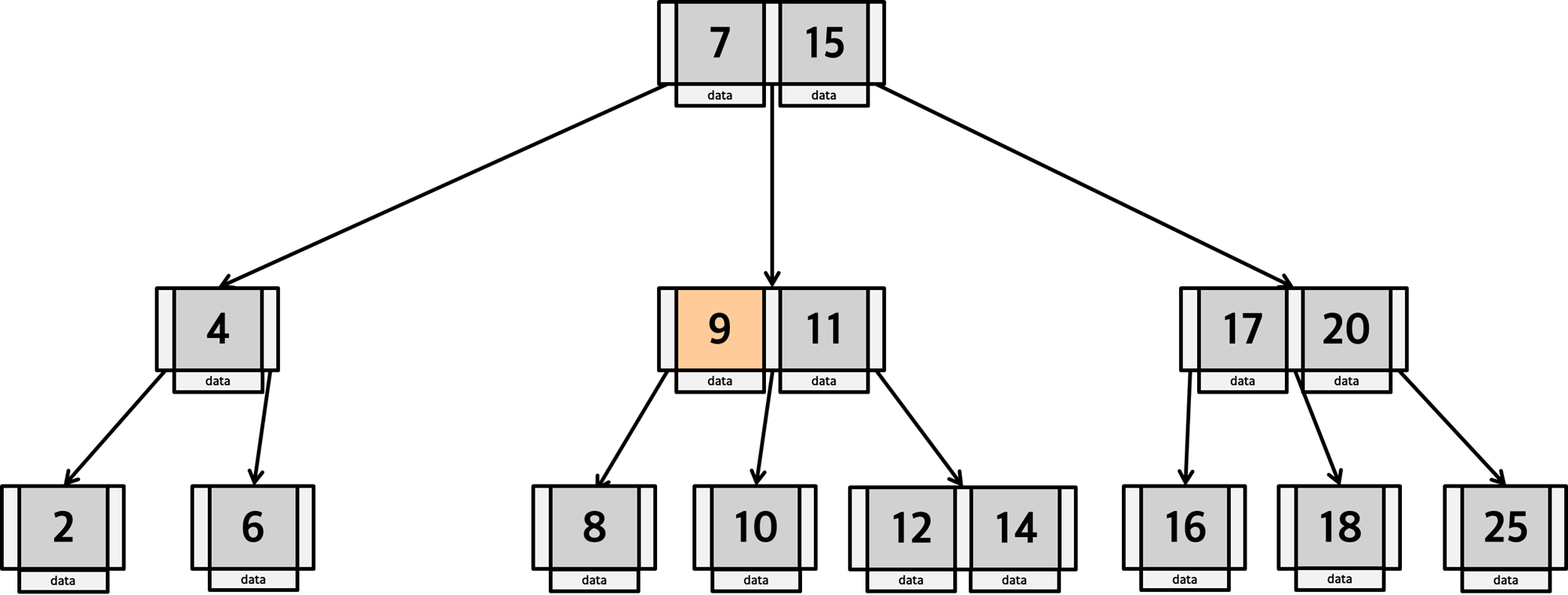
4. 11보다 크므로, 11의 오른쪽에 있는 포인터를 통해 자식으로 이동합니다.

5. 위와 같이 반복합니다. 12보다 크므로 다음 노드를 검사합니다.
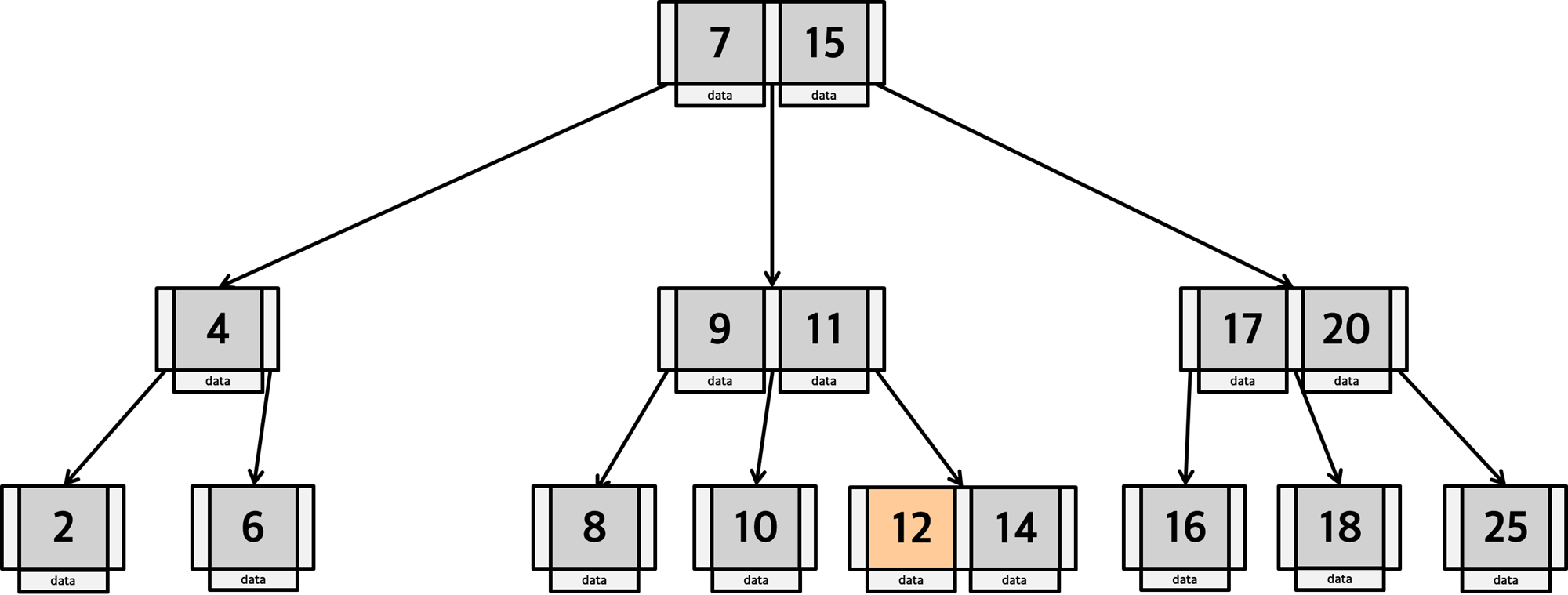
6. 14를 찾았으므로 해당 키의 데이터를 반환하고 탐색을 종료합니다.

B+Tree 탐색
B+Tree 탐색도 동일합니다. 루트 노드에서부터 해당 key를 찾아 주소를 타고 내려가죠.
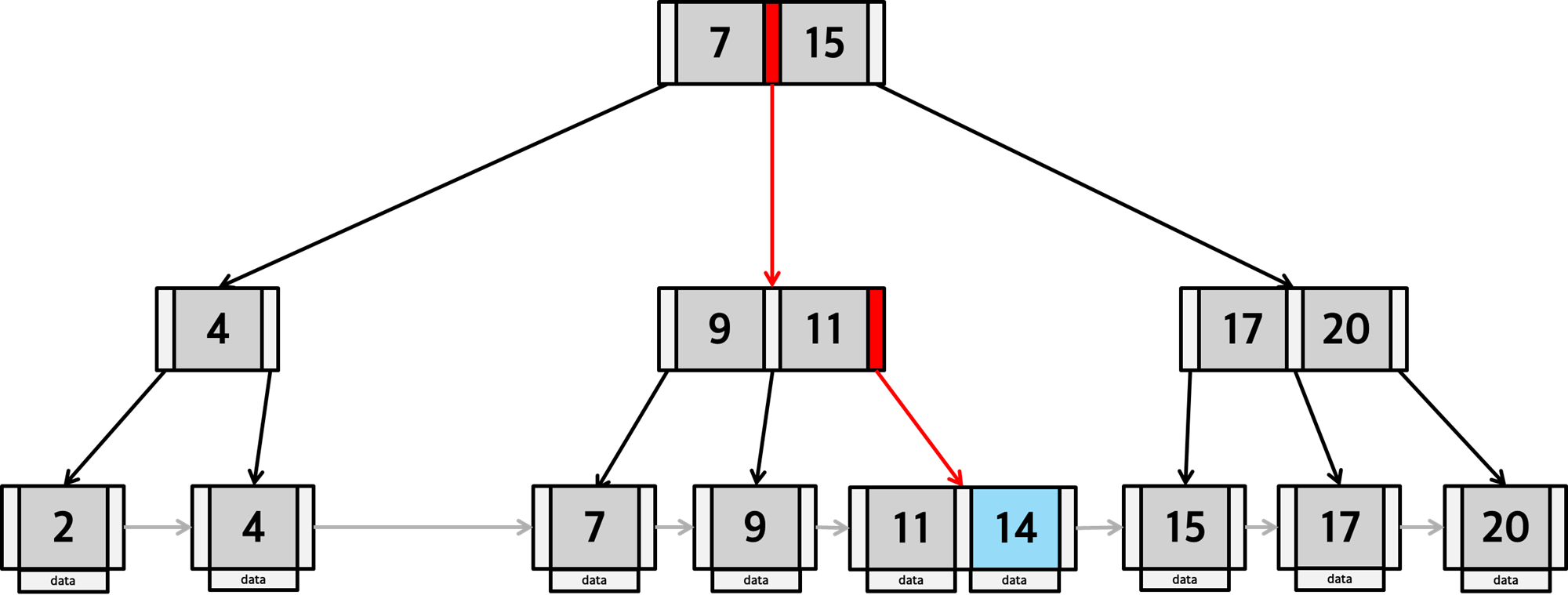
범위 탐색
여기서 14가 아니라 14부터 20까지의 key를 조회하고 싶다면, 즉 범위 탐색(검색)이 들어온다면 어떻게 될까요? 🤔
B-트리의 경우, 루트노드에 값이 존재한다면 바로 찾을 수 있다는 장점이 있습니다.
아래 예시에서 15는 바로 찾을수 있겠네요.

하지만 리프 노드에 찾으려는 key가 있을 경우 탐색 시간이 길어집니다.
인접 노드라도 다른 서브트리에 있다면 알 방법이 없기 때문이죠. 이때는 루트 노드에서 부터 다시 검사를 시작해야 합니다.

반대로 B+Tree는 리프노드에 모든 데이터가 저장되어있기 때문에, 값을 찾기위해 무조건 리프 노드까지 탐색해야 합니다.

하지만 인접한 노드를 알 수 있기 때문에 다른 서브트리에 존재하는 key를 찾기 위해 다시 루트부터 탐색하지 않고,
선형적으로 탐색 할 수 있습니다. 즉 B+Tree 는 순차 검색과 범위 검색에 더 좋은 성능을 보여주죠.
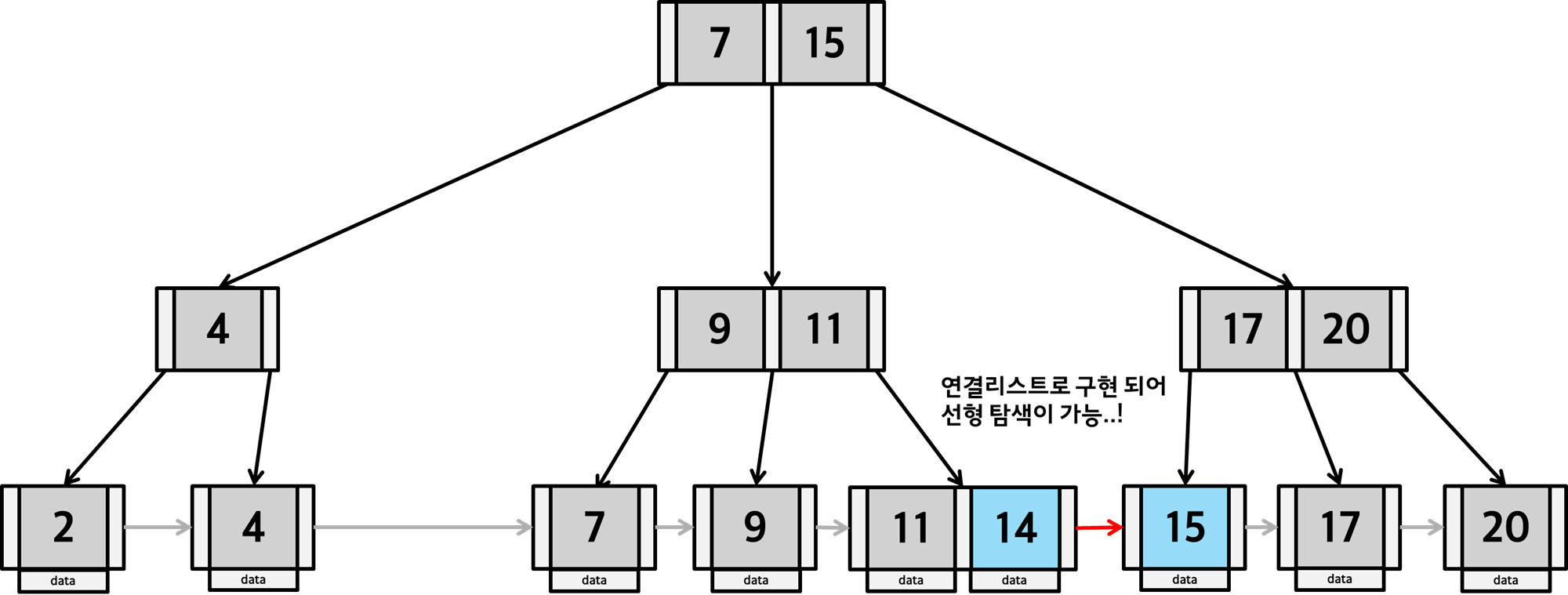
인덱스 컬럼은 부등호를 이용한 순차 검색 연산이 자주 발생할 수 있습니다.
B+Tree의 이용하면 순차 검색을 효율적으로 할 수 있으니 대부분의 DBMS는 B+ Tree 를 통해 인덱스를 구현하고 있는거죠. ⭐
삽입, 삭제 연산의 과정은 아래 참고자료에 잘 정리되어있으니, 관심있으신 분들은 한번 읽어보는 것을 추천합니다.
[참고자료]
감사합니다.
공부한 내용을 복습/기록하기 위해 작성한 글이므로 내용에 오류가 있을 수 있습니다.
'DB' 카테고리의 다른 글
| [DB] MySQL에서 UUID PK를 사용할 때 고려해야 할 점 (1) | 2024.04.04 |
|---|---|
| [DB] MySQL의 락 (feat. Auto Increment Lock) (0) | 2024.03.10 |
| [DB] 락(Lock)과 트랜잭션 (0) | 2024.03.09 |
| [DB] 정규형(Normal form) (0) | 2024.03.08 |
| [DB] 인덱스(Index) (0) | 2024.03.07 |
