티스토리 뷰
[인공지능] 머신러닝과 인공신경망 (feat. 분류, 회귀)
아래 글에 이어 작성된 글입니다. [인공지능] 전문가 시스템과 지식 아래글에 이어 작성된 글입니다. [인공지능] 탐색 아래글에 이어 작성된 글입니다. [인공지능] 인공지능과 딥러닝 [인공지능
munak.tistory.com
[인공지능] Numpy 기본 사용 + 딥러닝 express 연습문제 2장
아래 글에 이어 작성된 글입니다. [인공지능] 딥러닝과 Python 라이브러리 본격적으로 인공지능을 실습하기 전 Python의 여러 라이브러리를 소개합니다. Python(파이썬)은 머신러닝 프로젝트의 언어
munak.tistory.com
Scikit-learn을 사용한 기본 분류 예제 코드입니다.
Numpy만으로 퍼셉트론을 구현한 후 Sklearn의 성능과 비교합니다.
Scikit-learn
Scikit-learn(사이킷런)은 전통적인 머신러닝 라이브러리입니다. 다양한 분류 방법, 회귀, 클러스터링 등 대체로 클래식한 머신러닝 모듈을 지원합니다.
User guide: contents
User Guide: Supervised learning- Linear Models- Ordinary Least Squares, Ridge regression and classification, Lasso, Multi-task Lasso, Elastic-Net, Multi-task Elastic-Net, Least Angle Regression, LA...
scikit-learn.org
# pip
pip3 install -U scikit-learn
# conda
conda create -n sklearn-env -c conda-forge scikit-learn
conda activate sklearn-env
자주 사용되는 모듈들
데이터셋(datasets)
사이킷 런은 별도의 다운로드 없이 사용할 수 있는 표준 데이터 셋을 dataset 모듈로 제공하고 있습니다.
| 데이터셋 | 용도 | 설명 |
| load_boston( ) | - | 보스턴 주택가격 : 윤리적인 문제로 1.0 에서 더 이상 사용되지 않으며 1.2 에서 제거되었습니다. |
| load_iris( ) | 분류 | 붓꽃 데이터 |
| load_diabetes( ) | 회귀 | 당뇨병 환자 데이터 |
| load_digits( ) | 분류 | 0~9까지의 필기체 숫자 데이터 |
| load_linnerud( ) | - | 체력검사 데이터셋 (턱걸이, 앉았다 일어나기, 점프) |
| load_wine( ) | 분류 | 와인 데이터 |
| load_breast_cancer( ) | 분류 | 위스콘신 유방암 데이터 |
평가지표(Metrics)
평가지표는 모델의 성능을 평가(Evaluate)하는 방법들을 말합니다. 데이터셋에 따라 또 모델의 종류에 따라 여러 평가지표가 사용됩니다. 사이킷런 또한 여러 평가지표를 metrics 모듈을 통해 지원하고 있습니다. 해당 목록은 아래에서 확인 가능합니다.
3.3. Metrics and scoring: quantifying the quality of predictions
There are 3 different APIs for evaluating the quality of a model’s predictions: Estimator score method: Estimators have a score method providing a default evaluation criterion for the problem they ...
scikit-learn.org
sklearn.model_selection.train_test_split
머신러닝은 훈련 데이터와 테스트 데이터가 꼭 필요합니다. 하지만 매번 특정한 데이터들을 골라 테스트 데이터셋으로 분할하는 것은 굉장히 번거로운 일입니다. 이를 알아서 수행해주는 모듈이 train_test_split입니다.
sklearn.model_selection.train_test_split
Examples using sklearn.model_selection.train_test_split: Release Highlights for scikit-learn 0.24 Release Highlights for scikit-learn 0.24 Release Highlights for scikit-learn 0.23 Release Highlight...
scikit-learn.org
# example
import numpy as np
from sklearn.model_selection import train_test_split
X, y = np.arange(10).reshape((5, 2)), range(5)
# X
# array([[0, 1],
# [2, 3],
# [4, 5],
# [6, 7],
# [8, 9]])
# list(y)
# [0, 1, 2, 3, 4]
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=42)
# X_train
# array([[4, 5],
# [0, 1],
# [6, 7]])
# y_train
# [2, 0, 3]
# X_test
# array([[2, 3],
# [8, 9]])
# y_test
# [1, 4]
붓꽃 데이터 세트 분류 (KNN)
분류 알고리즘인 KNN을 사용해 붓꽃 데이터 세트를 분류하는 코드입니다.
1.6. Nearest Neighbors
sklearn.neighbors provides functionality for unsupervised and supervised neighbors-based learning methods. Unsupervised nearest neighbors is the foundation of many other learning methods, notably m...
scikit-learn.org
# 분류 정보를 세트로 저장
classes = {0:'setosa',1:'versicolor',2:'virginica'}
# 사이킷런 및 데이터 셋 적재
from sklearn import datasets
# 붓꽃 데이터 셋 저장
iris = datasets.load_iris()
# 훈련/테스트 데이터 분할 모듈 적재
from sklearn.model_selection import train_test_split
X = iris.data # 특징
y = iris.target # 출력
# (80:20)으로 분할
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=4)
# knn 분류 모듈 적재
from sklearn.neighbors import KNeighborsClassifier
# knn 모델 생성
knn = KNeighborsClassifier(n_neighbors=6)
# 모델 훈련
knn.fit(X_train, y_train)
# 훈련된 모델로 테스트 데이터 출력값을 예측
y_pred = knn.predict(X_test)
# 평가지수 모듈 적재
from sklearn import metrics
# 예측한 출력값과 실제출력간 정확도 계산
scores = metrics.accuracy_score(y_test, y_pred)
print(scores)
# 임의의 데이터생성
x_new = [[3,4,5,2], [5,4,2,2]]
# 앞서 훈련한 모델을 이용해 예측
y_predict = knn.predict(x_new)
# 세트를 사용해 모델로 예측한 결과를 레이블로 출력
print(classes[y_predict[0]])
print(classes[y_predict[1]])
0.9666666666666667
versicolor
setosa
+ 주석 없는 코드
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
classes = {0:'setosa',1:'versicolor',2:'virginica'}
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=4)
knn = KNeighborsClassifier(n_neighbors=6)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
scores = metrics.accuracy_score(y_test, y_pred)
print(scores)
x_new = [[3,4,5,2], [5,4,2,2]]
y_predict = knn.predict(x_new)
print(classes[y_predict[0]])
print(classes[y_predict[1]])
붓꽃 데이터셋 훈련 (Perceptron)
가. 사이킷런을 이용하여 학습 후 예측해보기
sklearn에서 제공하는 퍼셉트론 모듈을 이용해 붓꽃데이터를 학습시킨 후 setosa 품종인지 아닌지 이진 분류하는 코드입니다. 아나콘다에서 지원하는 spyder를 사용해 데이터 시각화 또한 진행해 보았습니다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Perceptron
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 붓꽃 데이터 받아오기
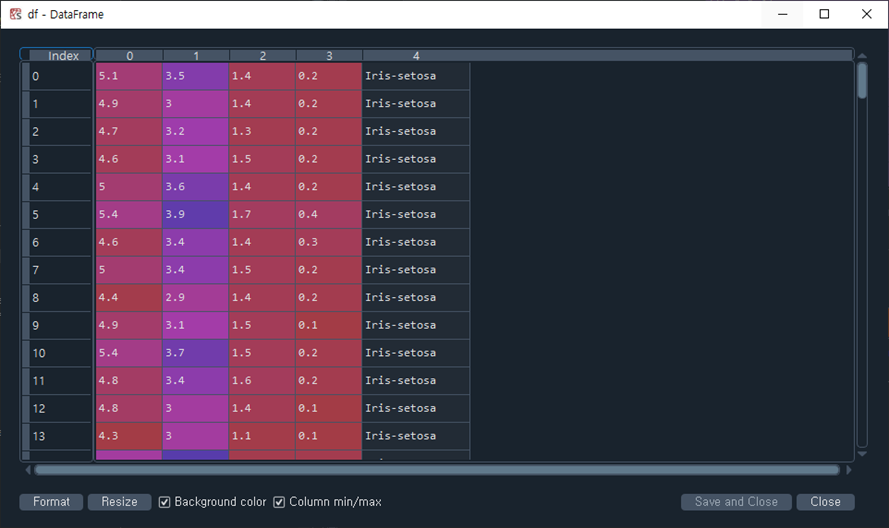
df = pd.read_csv('https://archive.ics.uci.edu/ml/' 'machine-learning-databases/iris/iris.data', header=None)
# setosa와 versicolor를 선택 : iloc[행, 열]
# 붓꽃 데이터 프레임에서 0부터 99까지 행의 4번째 열의 값을 가져와 y에 저장
# setosa와 versicolor은 0~99 행에 저장되어 있다.
y = df.iloc[0:100, 4].values
# y 정규화
# 값이 setosa이면 -1으로 아니면 1로 설정
y = np.where(y == 'Iris-setosa', -1.0, 1.0)
# 꽃받침 길이와 꽃잎 길이를 추출
# 붓꽃 데이터 프레임에서 0부터 99까지 행의 0, 2번째 열의 값을 가져와 X에 저장
X = df.iloc[0:100, [0, 2]].values
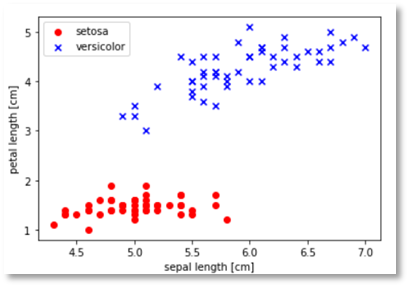
# 매트플롭을 이용해 산점도 그리기 | x축 : 꽃받침의 길이 | y축 : 꽃잎의 길이
plt.scatter(X[:50, 0], X[:50, 1], color='red', marker='o', label='setosa') # o : setosa
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor') # x : versicolor
plt.xlabel('sepal length [cm]') # 축 표시
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left') # 범례 표시(왼쪽위에)
plt.show() # 시각적으로 보이기
# 훈련데이터 셋, 테스트 데이터셋 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 사이킷 런을 이용한 퍼센트론 생성
ppn = Perceptron(max_iter=10, eta0=0.1, random_state=0)
# 학습
ppn.fit(X_train, y_train)
# 테스트 (예측)
y_pred = ppn.predict(X_test)
# 테스트 정확도 확인
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))
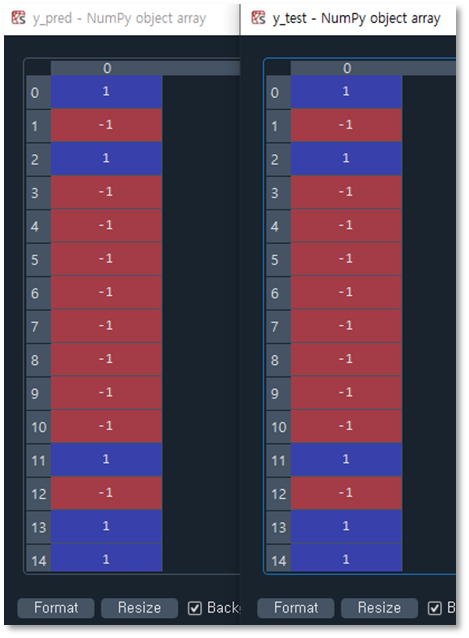
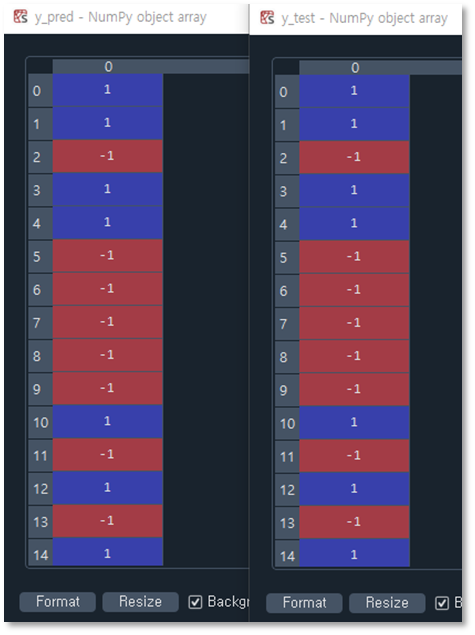
붓꽃 데이터에서 setosa와 versicolor를 추출하여 데이터 셋으로(train : test = 70: 30) 만들고 사이킷런을 이용해 학습을 진행하였습니다. 학습률은 0.1, epoch는 10으로 설정하였습니다. 출력 결과 정확도가 거의 1.00에 가까운 것을 확인할 수 있었으며 아래는 y_pred (예측 결과)와 y_test (실제 출력)의 비교 이미지입니다.
나. 순수 파이썬만을 이용하여 아래와 같은 그래프를 출력해보기
Epoch가 진행됨에 따라 달라지는 오차 발생 횟수를 그래프로 그리는 코드입니다. sklearn을 사용하지 않고 넘파이 만을 이용해 구현하였습니다.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import numpy as np
import math
# 퍼셉트론 클래스
class Perceptron(object):
# 생성자
def __init__(self, eta=0.1, n_iter=50):
self.eta = eta # 학습률
self.n_iter = n_iter # 학습 반복 회수 : epoch
# 학습 메소드
def fit(self, X, y):
# 0.0 ~ 1.0 난수로 가중치 초기화
self.w_ = np.random.random(size=1 + X.shape[1])
self.errors_list = [] # 발생 회수 저장
for _ in range(self.n_iter): # epoch만큼 반복
err = 0 # 오차 카운트 변수 선언
for x, target in zip(X, y): # 반복자 패턴 사용
update = self.eta * (target - self.predict(x)) # (학습률 * 오차) 계산
# print((target - self.predict(x)))
# 업데이트가 되었다면 : 오차가 있는것으로 오차 카운트
if update != 0.0:
err += 1
self.w_[1:] += update * x # 가중치 업데이트
self.w_[0] += update # 가중치(바이어스) 업데이트
self.errors_list.append(err) # 오차 카운트 리스트에 저장
return self # 객체 반환
# 내적 계산
def get_z(self, X):
return np.dot(X, self.w_[1:] + self.w_[0]) # 바이어스 가중치는 따로 계산
# 입력에 대한 결과 출력
def predict(self, X):
return np.round(math.tanh(self.get_z(X)), 2)
df = pd.read_csv('https://archive.ics.uci.edu/ml/' 'machine-learning-databases/iris/iris.data', header=None)
# setosa와 versicolor를 추출해 y에 저장
y = df.iloc[0:100, 4].values
# y 데이터 정규화
y = np.where(y == 'Iris-setosa', -1, 1)
# 꽃받침 길이와 꽃잎 길이를 추출해 X에 저장
X = df.iloc[0:100, [0, 2]].values
# 퍼셉트론 생성
ppn = Perceptron(eta=0.1, n_iter=10) # 학습률 0.1, epoch 10
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 학습
ppn.fit(X_train, y_train)
# Epochs에 대한 손실 변화 그래프 생성
plt.plot(range(1, len(ppn.errors_list) + 1), ppn.errors_list, marker='o')
# 그래프 x좌표 라벨 설정
plt.xlabel('Epochs')
# 그래프 y좌표 라벨 설정
plt.ylabel('Number of errors')
# 화면에 그래프 출력
plt.show()
퍼셉트론 클래스를 따로 만들어 필요한 생성자와 메소드를 작성하였습니다. 생성자에서는 학습률과 반복 횟수인 epoch를 받아 객체를 생성하며, 학습 메소드인 fit에서는 먼저 가중치를 기록할 넘파이 행렬 w_를 random 메소드를 통해 가중치에 적절한 0.0~1.0 사이의 값으로 초기화 합니다. 오차 발생 회수를 저장하기 위한 errors_list도 선언하고 epoch만큼 반복하며 퍼셉트론 가중치 갱신 알고리즘을 실행합니다. 이때 오차가 0.0이 아니라면, 즉 오차가 발생했다면 err변수를 증가시키고 한 epoch가 끝날 때 errors_list에 기록합니다. 내적 계산은 get_z 메소드를 만들어 처리하였고, 입력에 따른 예측 결과는 predict에서 계산할 수 있도록 하였습니다. 데이터에 음수 값이 들어가 있기 때문에 활성화 함수로는 tanh를 사용하였습니다. (0보다 작을 때에는 -1을 0보다 크거나 작을 때에는 1을 반환하게 하면 예시와 비슷한 그래프가 출력되는 것을 확인하였으나, 탄젠트 함수가 오차를 줄여가는 과정을 더 잘 보여준다고 생각해 아래와 같이 작성하였습니다.)
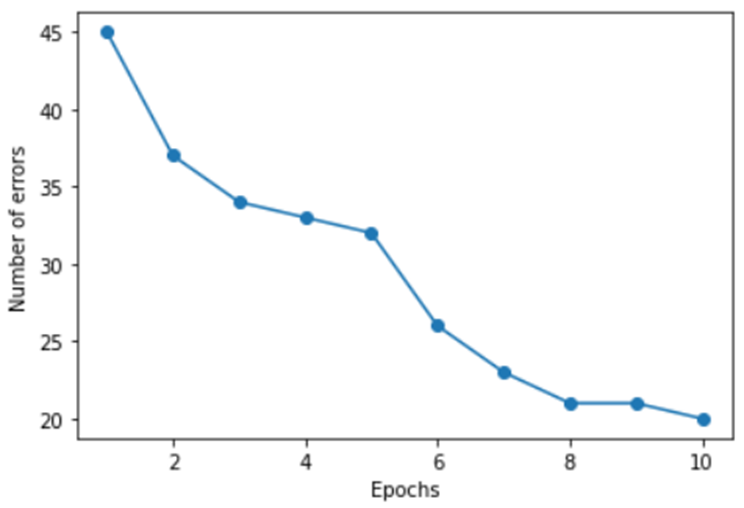
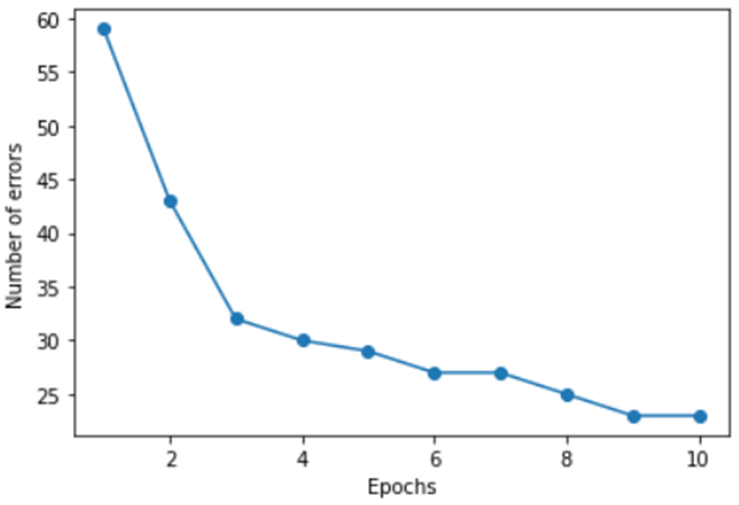
필기체 숫자 분류
위와 동일하게 분류 알고리즘인 KNN을 사용해 필기체 숫자 데이터 세트를 분류하는 코드입니다.
# 모듈 적재
import matplotlib.pyplot as plt # 맷플롯립
from sklearn import datasets, metrics # 사이킷런 데이터셋, 평가모듈
from sklearn.model_selection import train_test_split # 데이터 분류
# 필기체 숫자 데이터 셋 적재
digits = datasets.load_digits()
# 0번째 데이터(이미지) 확인
plt.imshow(digits.images[0], cmap=plt.cm.gray_r, interpolation='nearest')
# 전체 이미지 개수 저장
n_samples = len(digits.images)
# 이미지 전처리(평탄화)
data = digits.images.reshape((n_samples, -1))
# 훈련데이터와 테스트 데이터로 분할 (80:20)
X_train, X_test, y_train, y_test = train_test_split(data, digits.target, test_size=0.2)
# knn 모듈 적재
from sklearn.neighbors import KNeighborsClassifier
# knn 모델 생성
knn = KNeighborsClassifier(n_neighbors=6)
# 훈련데이터를 이용해 knn 모델 훈련
knn.fit(X_train, y_train)
# 테스트 데이터로 예측
y_pred = knn.predict(X_test)
# 정확도 계산
scores = metrics.accuracy_score(y_test, y_pred)
print(scores)
# 맷플롯립을 이용해 테스트 이미지 출력
# 이미지를 출력을 위해 평탄화된 이미지를 다시 8×8 형상으로 변환
plt.imshow(X_test[10].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
# 테스트 데이터 예측
y_pred = knn.predict([X_test[10]])
print(y_pred)

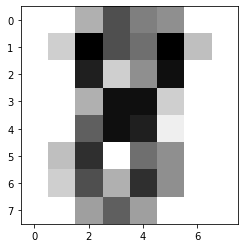
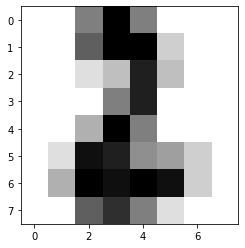
# 3번 실행 결과
0.9861111111111112
[0]
0.9777777777777777
[8]
0.9805555555555555
[2]
+ 주석 없는 코드
import matplotlib.pyplot as plt
from sklearn import datasets, metrics
from sklearn.model_selection import train_test_split
digits = datasets.load_digits()
plt.imshow(digits.images[0], cmap=plt.cm.gray_r, interpolation='nearest')
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
X_train, X_test, y_train, y_test = train_test_split(data, digits.target, test_size=0.2)
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=6)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
scores = metrics.accuracy_score(y_test, y_pred)
print(scores)
plt.imshow(X_test[10].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
y_pred = knn.predict([X_test[10]])
print(y_pred)
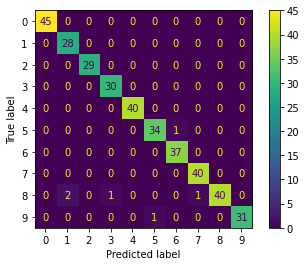
혼동 행렬(Confusion Matrix) 및 분류 리포트(classification_report) 출력하기
혼동 행렬은 분류(Classifier) 모델의 예측값과 실제 값의 교차표를 말하며 행렬 값들을 조합해 학습 성능을 평가 및 비교하는데에 사용됩니다. 분류 리포트 동일하게 성능 평가에 사용되며 여러 평가지표들을 요약해 보여줍니다. 다음은 출력 예시입니다.
# 모듈 적재
import matplotlib.pyplot as plt
from sklearn import datasets, metrics
from sklearn.model_selection import train_test_split
# 데이터셋 적재 및 전처리
digits = datasets.load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
# knn 모델 생성
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=6)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(
data, digits.target, test_size=0.2)
# 모델 학습
knn.fit(X_train, y_train)
# 테스트 데이터 예측
y_pred = knn.predict(X_test)
# 혼돈 행렬 출력
disp = metrics.plot_confusion_matrix(knn, X_test, y_test)
plt.show()
# 분류 리포트 출력
print(f"{metrics.classification_report(y_test, y_pred)}\n")
FutureWarning: Function plot_confusion_matrix is deprecated; Function `plot_confusion_matrix` is deprecated in 1.0 and will be removed in 1.2. Use one of the class methods: ConfusionMatrixDisplay.from_predictions or ConfusionMatrixDisplay.from_estimator.
warnings.warn(msg, category=FutureWarning)
precision recall f1-score support
0 1.00 1.00 1.00 45
1 0.93 1.00 0.97 28
2 1.00 1.00 1.00 29
3 0.97 1.00 0.98 30
4 1.00 1.00 1.00 40
5 0.97 0.97 0.97 35
6 0.97 1.00 0.99 37
7 0.98 1.00 0.99 40
8 1.00 0.91 0.95 44
9 1.00 0.97 0.98 32
accuracy 0.98 360
macro avg 0.98 0.98 0.98 360
weighted avg 0.98 0.98 0.98 360
직선의 기울기와 y절편 구하기
선형회귀 모듈을 이용해 임의의 점 3개에 근접하는 직선의 기울기와 절편을 구합니다.
# 모듈 적재
import matplotlib.pylab as plt
from sklearn import linear_model
# 선형 회귀 모델 생성
reg = linear_model.LinearRegression()
# 파이썬 리스트, 넘파이 배열 모두 사용가능하다.
X = [[0], [1], [2]] # 2차원 배열을 사용
y = [3, 4.5, 5.5]
# 모델 학습
reg.fit(X, y)
print(reg.coef_) # 직선의 기울기 출력
print(reg.intercept_) # 직선의 y-절편 출력
print(reg.score(X, y)) # 평가지수 출력
# x=5에 대한 예측값 출력
print(reg.predict([[5]]))
# 학습 데이터와 y 값을 산포로 출력
plt.scatter(X, y, color='black')
# 학습 데이터를 입력으로 하여 예측값을 계산
y_pred = reg.predict(X)
# 학습 데이터와 예측값으로 선그래프로 출력
# 계산된 기울기와 y 절편을 가지는 직선 출력
plt.plot(X, y_pred, color='blue', linewidth=3)
plt.show()
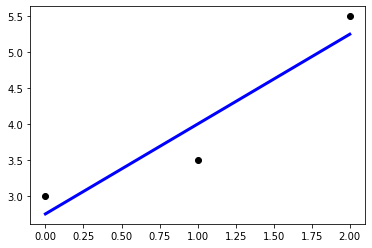
[1.25] # 기울기
2.7500000000000004 # y절편
0.8928571428571429 # 정확도
[9.] # x=5 예측 결과
+ 주석 없는 코드
import matplotlib.pylab as plt
from sklearn import linear_model
reg = linear_model.LinearRegression()
X = [[0], [1], [2]]
y = [3, 3.5, 5.5]
reg.fit(X, y)
print(reg.coef_)
print(reg.intercept_)
print(reg.score(X, y))
print(reg.predict([[5]]))
plt.scatter(X, y, color='black')
y_pred = reg.predict(X)
plt.plot(X, y_pred, color='blue', linewidth=3)
plt.show()
치즈에 대한 맛 검정
퍼셉트론을 통해 치즈의 지방과 염분 데이터를 통해 치즈 맛에 대한 검정을 수행합니다.
- 입력 데이터
| 0.2 | 0.9 | (Like) 1 |
| 0.1 | 0.1 | (DisLike) -1 |
| 0.2 | 0.4 | (DisLike) -1 |
| 0.2 | 0.5 | (DisLike) -1 |
| 0.4 | 0.5 | (Like) 1 |
| 0.3 | 0.8 | (Like) 1 |
- 초기 가중치, 학습률
| -0.30 | 0.05 | 0.01 | 0.2 |
가. 사이킷런으로 학습하여 예측 후 정확률을 출력하라
from sklearn.linear_model import Perceptron
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 데이터
X = [[0.2, 0.9],[0.1, 0.1],[0.2, 0.4],[0.2, 0.5],[0.4, 0.5], [0.3, 0.8]]
y = [1.0, -1.0, -1.0, -1.0, 1.0, 1.0]
# 훈련데이터 셋, 테스트 데이터셋 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 사이킷 런을 이용한 퍼센트론 생성
ppn = Perceptron(eta0=0.2, random_state=0, max_iter=40)
# 학습
ppn.fit(X_train, y_train)
# 테스트 (예측)
y_pred = ppn.predict(X_test)
# 테스트 정확도 확인
print('Accuracy: %.2f' % accuracy_score(y_test, y_pred))
먼저 제시된 데이터를 리스트에 저장하고, train_test_split로 훈련 데이터와 테스트 데이터를 80:20으로 분리하였습니다. 그리고 sklearn에서 지원하는 Perceptron 클래스를 사용하여 학습률 0.2, epoch 40을 가진 퍼셉트론을 생성하여 학습을 진행한 뒤 모델에 테스트 데이터(X_test)를 넣고 출력과 실제 정답의 정확률을 확인하였습니다.
Python 3.7.11 (default, Jul 27 2021, 09:42:29) [MSC v.1916 64 bit (AMD64)]
Type "copyright", "credits" or "license" for more information.
IPython 7.31.1 -- An enhanced Interactive Python.
Accuracy: 0.50
Accuracy: 1.00
Accuracy: 0.50
Accuracy: 0.00
Accuracy: 0.50
여러 번 실행한 결과 다음과 같은 정확도가 나오는 것을 볼 수 있었습니다. 충분히 많은 학습 데이터가 제공된다면 더 좋은 결과가 나왔을 것으로 예상됩니다.
나. 순수 파이썬으로 퍼셉트론 구현후, 가중치 w0, w1, w2를 계산 후 출력하라.
import numpy as np
import math
# 부동소수점 오차 방지
epsilon = 0.0000001
# 훈련 데이터 셋
X = np.array([
[1.0, 0.2, 0.9], # 1은 바이어스를 위한 입력값
[1.0, 0.1, 0.1],
[1.0, 0.2, 0.4],
[1.0, 0.2, 0.5],
[1.0, 0.4, 0.5],
[1.0, 0.3, 0.8]
])
y = np.array([1.0, -1.0, -1.0, -1.0, 1.0, 1.0])
# 가중치 저장
W = np.array([-0.30, 0.05, 0.01])
# 퍼셉트론 학습 알고리즘
def perceptron_fit(X, Y, epochs):
global W
r = 0.2 # 학습률
# epoch 만큼 반복
for k in range(epochs):
print("========== epoch :", k, "===========")
for i in range(len(X)):
print("[1, x1, x2] =", X[i])
print("[w0(b), w1, w2] =", np.round(W, 2))
z = np.dot(X[i], W); # 내적 구하기
print("z : {:.2f}".format(z))
predict = math.tanh(z) # 활성화 함수 실행 : tan
print("y : {:.2f}".format(predict))
print("Y :", Y[i])
error = round(Y[i] - predict, 2) # 오차 계산
print("Y-y=", error)
print("r*(Y-y) : {:.2f}".format(r * error))
Tem_W = np.round(W, 2)
W += r * error * X[i] # 가중치 업데이트
print("[∆w0(b), ∆w1, ∆w2] =", np.round((Tem_W - W), 2))
print("--------------------------------")
# 예측 함수
def perceptron_predict(X, Y):
global W
for x in X: # 입력에 대한 출력값 확
print(x[1], x[2], "->", np.round(math.tanh(np.dot(x, W)), 2))
perceptron_fit(X, y, 1)
perceptron_predict(X, y)
순수 파이썬 + 넘파이를 사용해 입력 데이터와 epoch를 매개변수로 실행되는 퍼셉트론 학습 알고리즘을 구현하였습니다. 활성화 함수는 math클래스의 tanh를 이용해 탄젠트 함수로 구현하였으며, 실제 값들의 변화를 살펴보고 계산 과정을 구현하면서 퍼셉트론의 가중치 갱신 알고리즘 “새로운 가중치 = 이전 가중치 + 학습률 * (정답-예측값) * 학습 데이터”를 복습할 수 있었습니다.
...
y : -0.20
Y : -1.0
Y-y= -0.8
r*(Y-y) : -0.16
[∆w0(b), ∆w1, ∆w2] = [0.16 0.03 0.08]
--------------------------------
[1, x1, x2] = [1. 0.4 0.5]
[w0(b), w1, w2] = [-2.34 2.08 3.02]
z : 0.00
y : 0.00
Y : 1.0
Y-y= 1.0
r*(Y-y) : 0.20
[∆w0(b), ∆w1, ∆w2] = [-0.2 -0.08 -0.1 ]
--------------------------------
[1, x1, x2] = [1. 0.3 0.8]
[w0(b), w1, w2] = [-2.14 2.16 3.12]
z : 1.00
y : 0.76
Y : 1.0
Y-y= 0.24
r*(Y-y) : 0.05
[∆w0(b), ∆w1, ∆w2] = [-0.05 -0.02 -0.03]
--------------------------------
0.2 0.9 -> 0.83
0.1 0.1 -> -0.91
0.2 0.4 -> -0.37
0.2 0.5 -> -0.08
0.4 0.5 -> 0.34
0.3 0.8 -> 0.8
# 정답 [1.0, -1.0, -1.0, -1.0, 1.0, 1.0]
위는 40번을 반복 학습(40epoch)한 후 입력 데이터에 대한 출력 결과입니다. 학습이 잘 이루어져 정답에 근사한 것을 볼 수 있습니다. 이어서 1epoch의 출력 결과를 바탕으로 제시된 표를 채우면 아래와 같습니다.
========== epoch : 0 ===========
[1, x1, x2] = [1. 0.2 0.9]
[w0(b), w1, w2] = [-0.3 0.05 0.01]
z : -0.28
y : -0.27
Y : 1.0
Y-y= 1.27
r*(Y-y) : 0.25
[∆w0(b), ∆w1, ∆w2] = [-0.25 -0.05 -0.23]
--------------------------------
[1, x1, x2] = [1. 0.1 0.1]
[w0(b), w1, w2] = [-0.05 0.1 0.24]
z : -0.01
y : -0.01
Y : -1.0
Y-y= -0.99
r*(Y-y) : -0.20
[∆w0(b), ∆w1, ∆w2] = [0.19 0.02 0.02]
...
--------------------------------
0.2 0.9 -> 0.33
0.1 0.1 -> 0.01
0.2 0.4 -> 0.14
0.2 0.5 -> 0.18
0.4 0.5 -> 0.22
0.3 0.8 -> 0.31
| B | Fat | Salt | w0(b) | w1 | w2 | z | f(z) = y | y | (Y-y) | r*(Y-y) | ∆w0(b) | ∆w1 | ∆w2 |
| 1 | 0.2 | 0.9 | -0.30 | 0.05 | 0.01 | -0.28 | -0.27 | 1 | 1.27 | 0.25 | -0.25 | -0.05 | -0.23 |
| 1 | 0.1 | 0.1 | -0.05 | 0.10 | 0.24 | -0.01 | -0.01 | -1 | -0.99 | -0.20 | 0.19 | 0.02 | 0.02 |
| 1 | 0.2 | 0.4 | -0.24 | 0.08 | 0.22 | -0.14 | -0.14 | -1 | -0.86 | -0.17 | 0.18 | 0.03 | 0.07 |
| 1 | 0.2 | 0.5 | -0.42 | 0.05 | 0.15 | -0.33 | -0.32 | -1 | -0.68 | -0.14 | 0.13 | 0.03 | 0.07 |
| 1 | 0.4 | 0.5 | -0.55 | 0.02 | 0.08 | -0.50 | -0.46 | 1 | 1.46 | 0.29 | -0.29 | -0.12 | -0.15 |
| 1 | 0.3 | 0.8 | -0.26 | 0.14 | 0.23 | -0.04 | -0.04 | 1 | 1.04 | 0.21 | -0.21 | -0.06 | -0.16 |
MNIST
MNIST 를MLP를 이용하여 학습시키자. KNN, 단층퍼셉트론과 다층퍼셉트론의 결과를 비교해보자.
MNIST 데이터 셋을 KNN, Perceptron(단층퍼셉트론), MLP(다층퍼셉트론)로 학습시켜 비교해 보았습니다. sklearn 의 KneighborsClassifier, Perceptron, MLPClassifier 클래스를 이용하여 각각의 모델을 생성하였으며, 퍼셉트론과 MLP의 경우 학습률은 0.001로, epoch는 30,000으로 설정해 학습을 진행하였습니다.
또한 MNIST에서 제공하는 필기체 숫자데이터 세트 중에서 datasets.load_digits()를 통해 불러온 1,797개의 8x8 이미지 데이터와 mnist.load_data()를 통해 불러온 70,000개의 28x28 이미지에 대해 각각 학습 후 정확률을 출력해 보았습니다.
- datasets.load_digits()를 통한 1,797개의 8x8 이미지 데이터 사용
- 훈련데이터 : 테스트데이터 = 8 : 2
# Perceptron
from sklearn import datasets, metrics
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import Perceptron
from sklearn.neural_network import MLPClassifier
# 필기체 숫자 데이터 불러오기
digits = datasets.load_digits()
#plt.imshow(digits.images[0], cmap=plt.cm.gray_r, interpolation='nearest')
n_samples = len(digits.images) # 이미지의 총 픽셀 수
data = digits.images.reshape((n_samples, -1)) # 이미지 평탄화
# 훈련데이터 : 테스트데이터 = 8 : 2로 분할
X_train, X_test, y_train, y_test = train_test_split(data, digits.target, test_size=0.2)
# KNN 생성, 학습
knn = KNeighborsClassifier(n_neighbors=6).fit(X_train, y_train)
# 테스트 데이터로 예측 후 정확도 계산
y_pred_knn = knn.predict(X_test)
scores = metrics.accuracy_score(y_test, y_pred_knn)
print("KNN :", scores)
# Perceptron 생성, 학습
percept = Perceptron(random_state=1, eta0=0.001, max_iter=30000).fit(X_train, y_train)
# 테스트 데이터로 예측 후 정확도 계산
y_pred_percept = percept .predict(X_test)
scores = metrics.accuracy_score(y_test, y_pred_percept)
print("Perceptron :", scores)
# MLP생성, 학습
mlp = MLPClassifier(random_state=1, max_iter=30000).fit(X_train, y_train)
# 테스트 데이터로 예측 후 정확도 계산
y_pred_mlp = mlp.predict(X_test)
scores = metrics.accuracy_score(y_test, y_pred_mlp)
print("MLP : ",scores)
# 실행 1
KNN : 0.9777777777777777
Perceptron : 0.9444444444444444
MLP : 0.9555555555555556
# 실행 2
KNN : 0.9861111111111112
Perceptron : 0.9138888888888889
MLP : 0.9833333333333333
감사합니다.
공부한 내용을 복습/기록하기 위해 작성한 글이므로 내용에 오류가 있을 수 있습니다.
'인공지능' 카테고리의 다른 글
| [인공지능] Numpy로 역방향전파 구현하기 (1) | 2022.09.14 |
|---|---|
| [인공지능] 딥러닝 express 연습문제 4장 (1) | 2022.09.08 |
| [인공지능] Numpy로 경사하강법 구현하기 (0) | 2022.09.07 |
| [인공지능] Numpy 기본 사용 + 딥러닝 express 연습문제 2장 (0) | 2022.09.01 |
| [인공지능] 딥러닝과 Python 라이브러리 (0) | 2022.08.30 |
