티스토리 뷰
아래 글에 이어 작성된 글입니다.
[인공지능] 인공신경망의 시작, 퍼셉트론
아래 글에 이어 작성된 글입니다. [인공지능] 머신러닝과 인공신경망 아래 글에 이어 작성된 글입니다. [인공지능] 전문가 시스템과 지식 아래글에 이어 작성된 글입니다. [인공지능] 탐색 아래
munak.tistory.com
다층 퍼셉트론 MLP와 핵심인 역전파 알고리즘에 대한 내용을 다룹니다.
다층 퍼셉트론 : Multilayer Perceptron
다층 퍼셉트론(MLP)은 입력층과 출력층 사이에 은닉층이라는 새로운 층을 가지고 있는 퍼셉트론을 말합니다. 기존의 퍼셉트론의 경우 한 개의 뉴런 구조만을 가진 단순한 형태였으며, XOR을 학습하지 못하는 등의 한계점이 있었습니다. 연구자들은 우리의 뇌가 수백만 개의 뉴런들로 이루어져 있듯이 조금 더 복잡한 형태의 신경망을 만들어 퍼셉트론의 한계를 극복하고자 하였고, 그 결과 여러 개의 뉴런들이 이어진 형태의 다층 퍼셉트론이 만들어지게 되었습니다.

구조가 복잡해짐에 따라 기존의 퍼셉트론의 계산방식과는 다른 계산법이 필요해지게 되었고, 추가적인 연구를 통해 새로운 학습 알고리즘이 발견되었습니다. 바로 역전파 알고리즘입니다.
MLP의 학습알고리즘
기존의 퍼셉트론의 경우 입력이 주어질 때 결과값을 계산하고 발생하는 오차를 이용해 가중치를 변경시키는 방법을 사용했었습니다. MLP의 경우는 추가된 은닉층과 그 가중치들을 학습시키기 위해 다음과 같이 3단계를 거쳐 학습을 진행합니다.
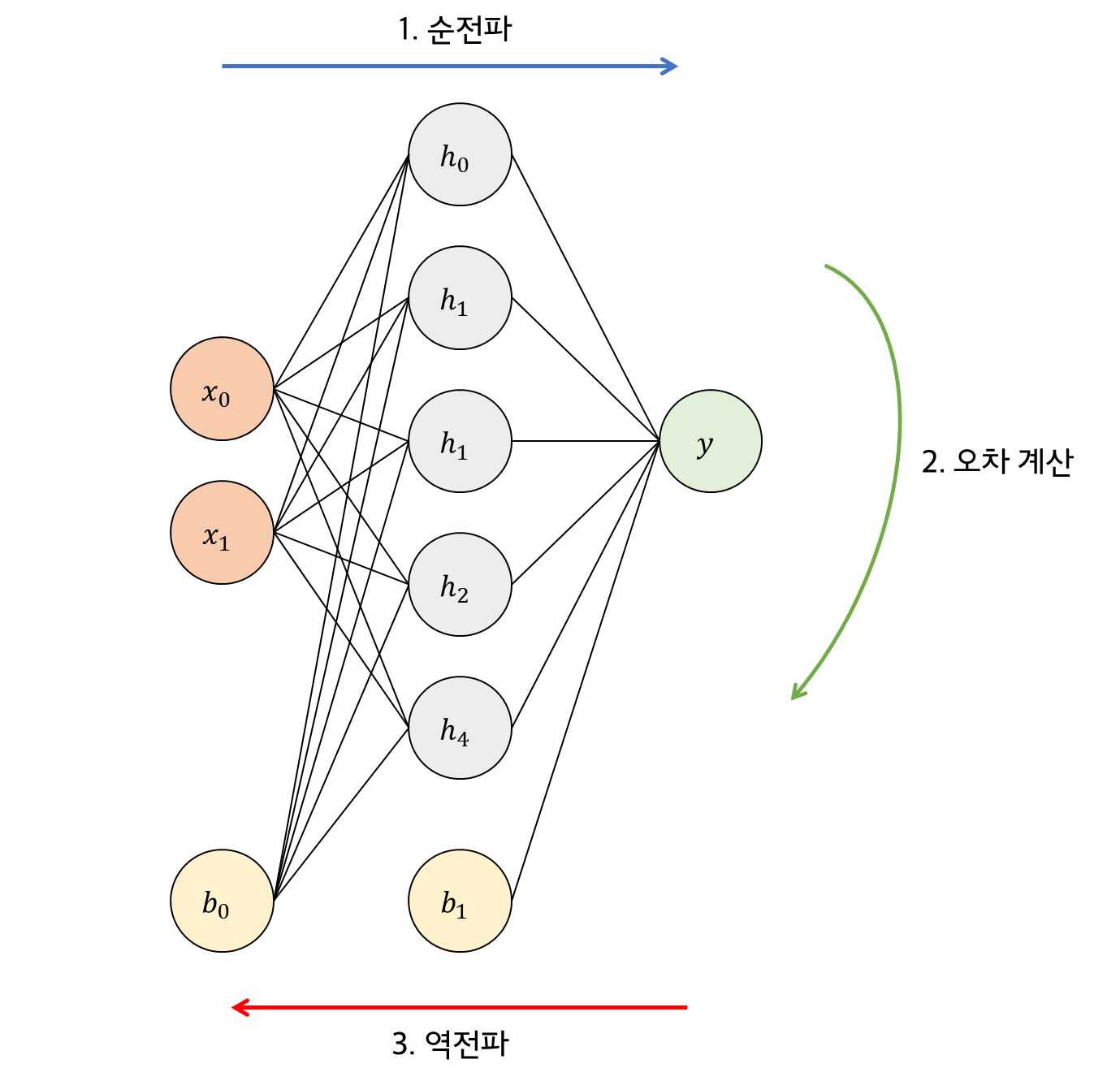
1단계 : 순전파
입력층에 주어진 입력을 순방향으로 전파시켜 출력을 계산한다.
2단계 : 오차계산
순전파를 통해 계산한 결과값(출력)과 정답간의 오차를 계산한다.
3단계: 역전파
오차를 이용해 신경망의 가중치와 바이이어스 값을 변경한다.
순전파 알고리즘
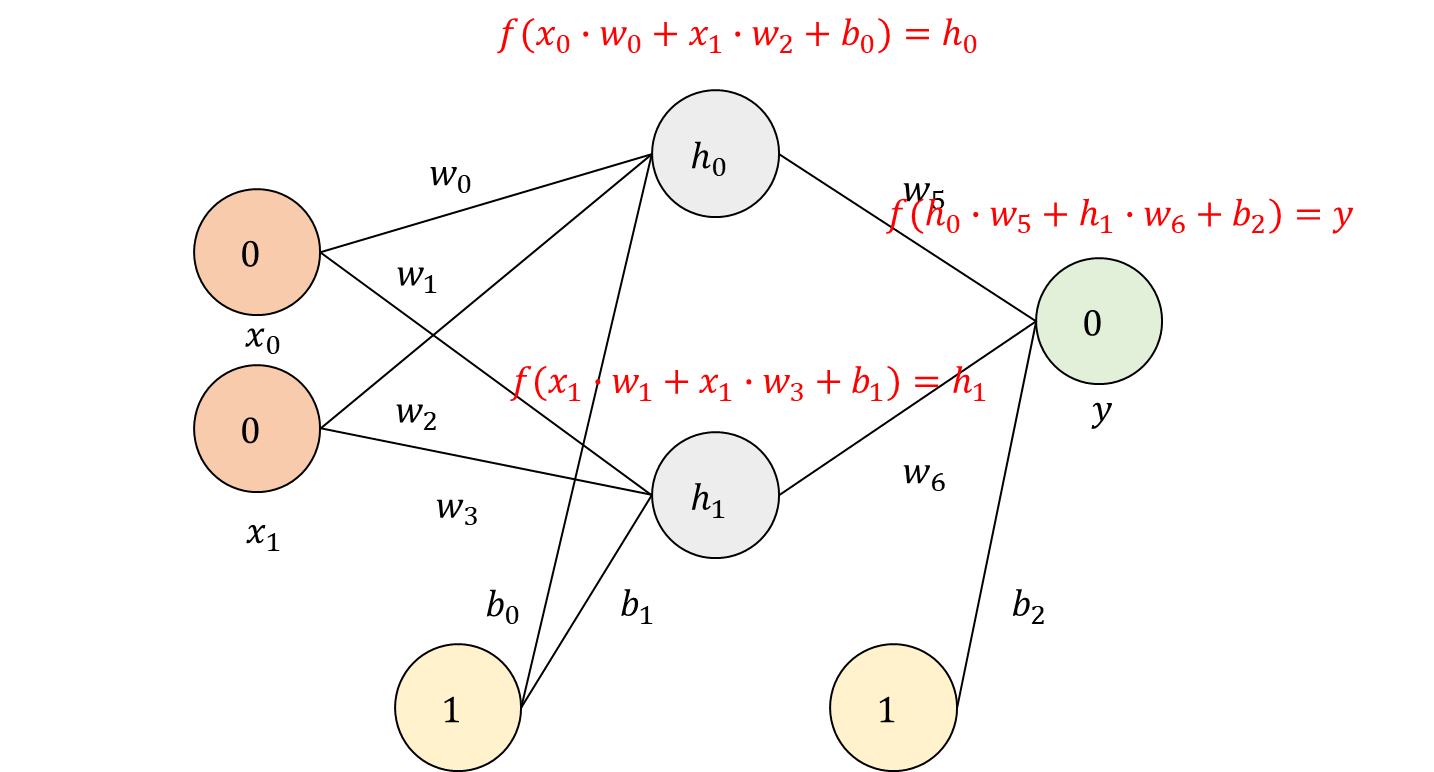
순전파 알고리즘부터 살펴보겠습니다. 기존의 퍼셉트론의 출력 계산 방법과 동일합니다. 입력값과 바이어스 값을 곱하고 활성화 함수를 통해 출력값을 계산하면 됩니다. 아래 구조를 예시로 \(h_{0}\)을 계산하면 다음과 같습니다.
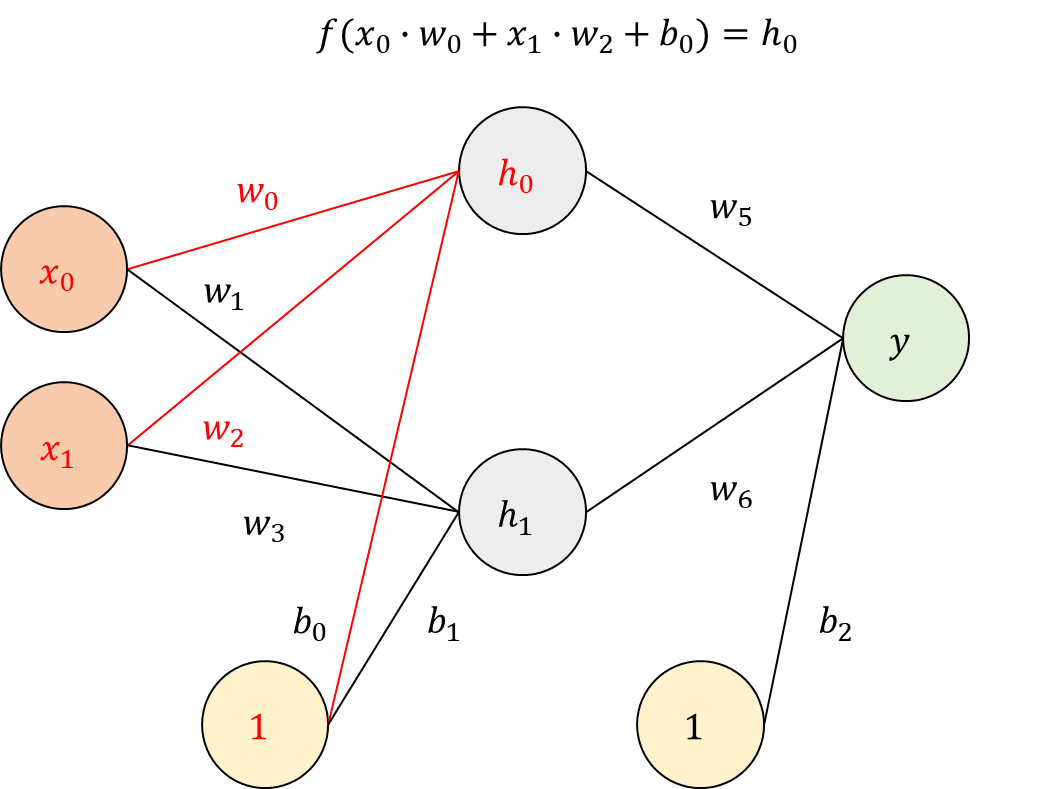
활성화 함수
퍼셉트론은 활성화 함수로 0보다 작으면 0을, 0보다 크면 1을 출력하는 계단 함수를 사용했었습니다. MLP에서는 다양한 함수들이 활성화 함수로 연구되어 사용되기 시작했습니다.
+ 모두 비선형 함수인데, 선형함수의 경우 여러 개의 층에 적용 시 의미가 없기 때문이다.
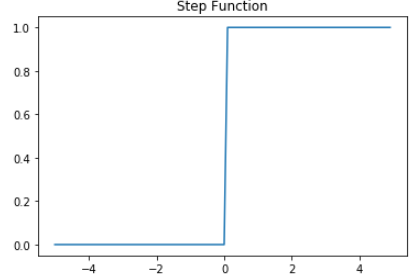
계단함수 (step function)
입력 신호의 총합이 0을 넘으면 1을, 아니라면 0을 출력한다.
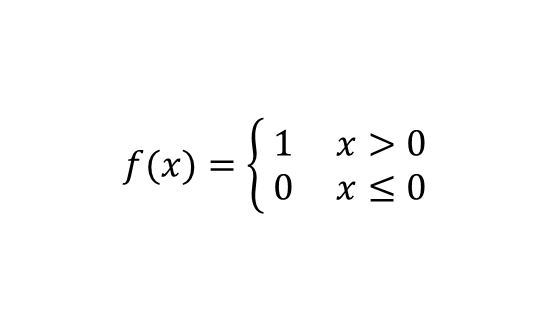
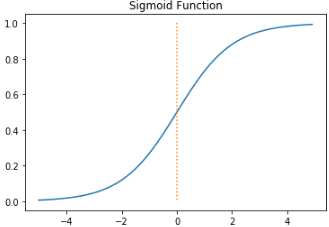
시그모이드 함수 (sigmoid function)
s자 형태의 곡선이며, 계단함수와 다르게 0에서 미분이 가능하다는 특징이 있다. 출력이 0.0에서 1.0의 연속적인 실수기 때문에 정밀한 출력이 가능하다.
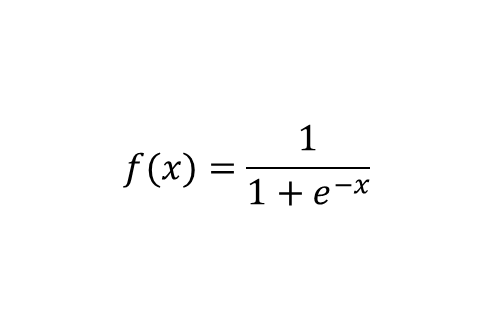

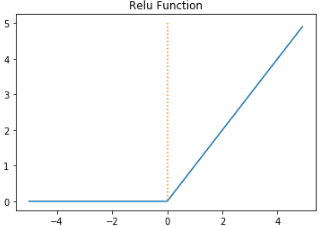
ReLU 함수 (Rectifed Linear Unit function)
0을 넘으면 값을 그대로 출력하고 아니라면 0을 출력하는 함수이다. 후에 나올 심층신경망의 그래디언트 소멸 문제를 방지해 널리 사용되고 있다.
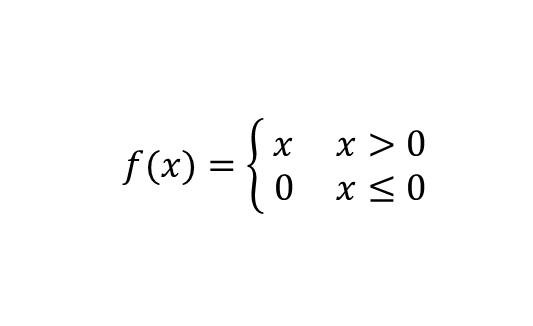

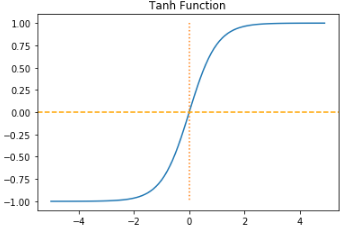
tanh 함수 (tangent function)
시그모이드 함수와 유사하나, 출력 값이 -1에서 1까지로 음수 출력을 지원한다.
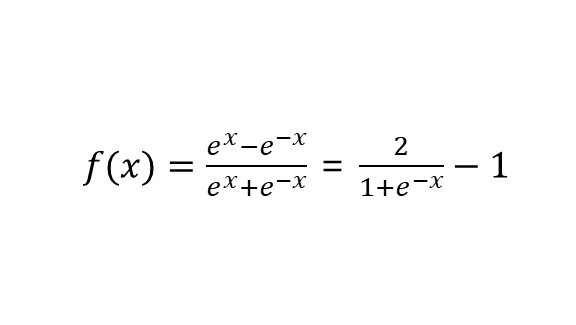

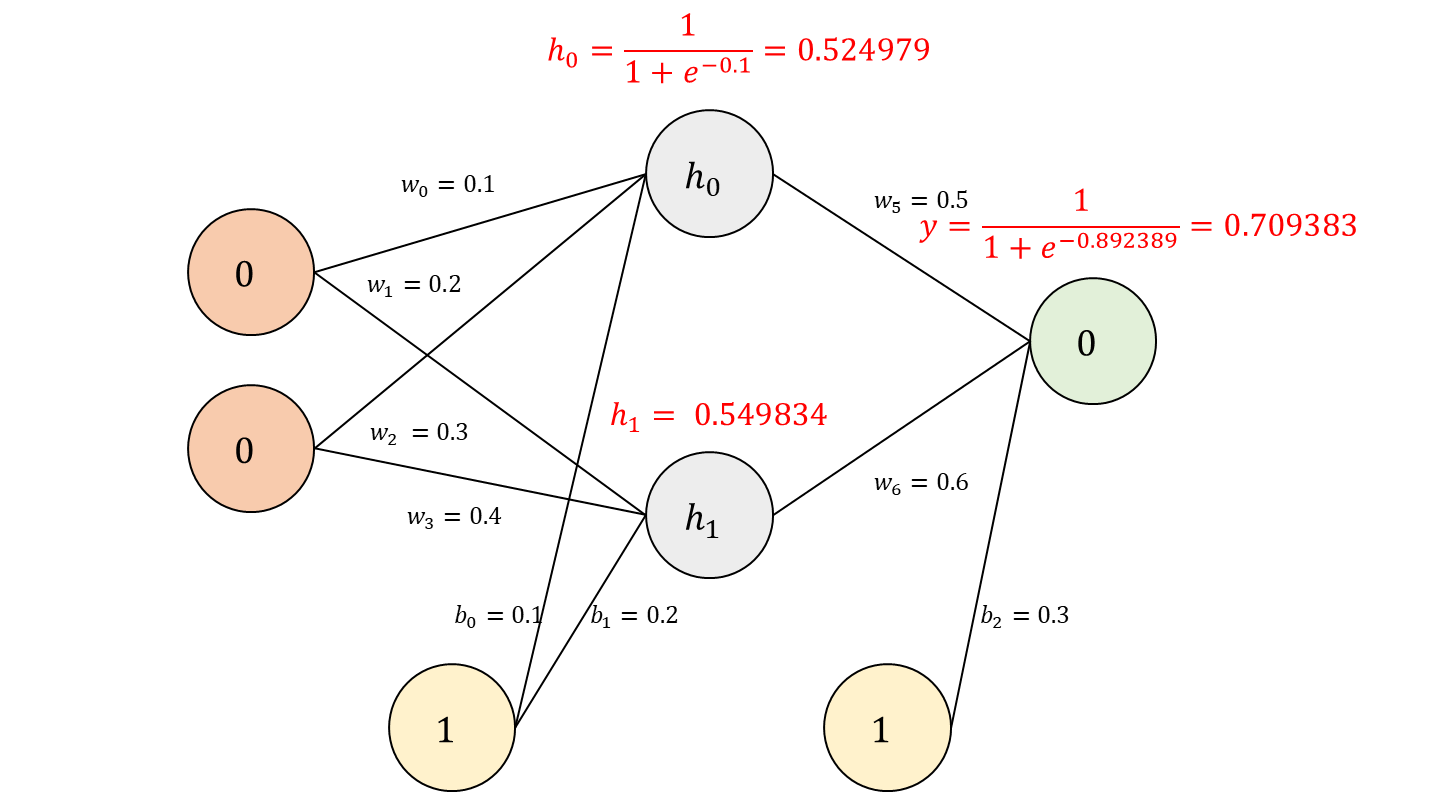
입력을 0, 0으로 출력이 0이면서 활성화 함수는 시그모이드 함수를, 가중치와 바이어스를 임의로 설정했을 때 예시를 계산해 보겠습니다.
출력 결과는 0.709383이 됩니다.
손실 함수
이어서 출력 결과를 바탕으로 오차를 구하는 방법을 알아보겠습니다. 오차는 정답과 출력의 차이로 신경망에서 학습의 성과를 나타내는 지표로 사용됩니다. 이때 손실을 계산하는 방법 또는 공식이 손실함수(\(E(w)\))이며 데이터에 따라, 구하고자 하는 결과에 따라 여러 손실함수가 사용되고 있습니다. 이번 글에서는 MLP 학습이 주내용이기 때문에 전통적인 손실함수 MSE만 다뤄보겠습니다.
MSE
MSE(Mean Squared Error)은 우리말로 해석하면 평균 제곱 오차로 아래 식을 따라 계산합니다. \(y_{i}\)는 출력층 유닛 i의 값이고 \(t_{i}\)는 정답일때 이들의 차의 제곱을 모두 더하고 나누어 주면 됩니다.
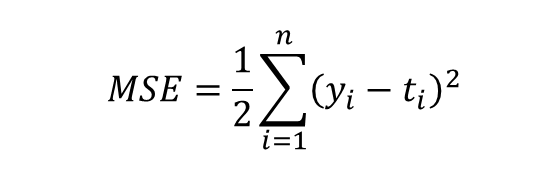
+ 2가 아닌 n나 다른 숫자로 나누는 경우가 있는데, MSE에서 중요한 값은 \((y_i - t_i)^2 \)으로 무엇으로 나누든 전체적인 성능에 큰 영향은 미치지 않는다고 합니다.
경사하강법
오차를 구했다면 이를 줄이는 방법을 찾아야 합니다. 그래야 학습이 될 테니까요. 이전 글에서 다룬 퍼셉트론의 경우 오차를 이용해 가중치를 변경하는 방법을 사용했었습니다. MLP에서는 경사하강법이 사용됩니다. 신경망에서 경사하강법은 손실함수의 1차 미분 값(그래디언트)을 사용해 가중치를 변경하는 것을 의미합니다.
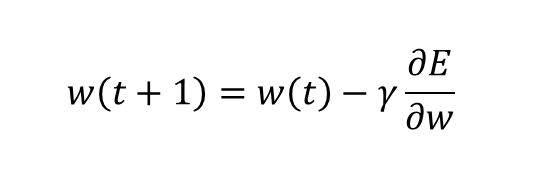
우리는 가중치를 변경해 전체 손실함수 값을 줄일 것이기 때문에 그래디언트는 가중치의 변화량분의 손실함수의 변화량으로 나타낼 수 있습니다. 즉 경사하강법은 수학적으로 손실함수가 최소값을 가지는 가중치 \(w\)를 찾는 문제로 귀결됩니다. (학습률의 역할은 기존의 퍼셉트론과 동일합니다.) 하지만 최솟값을 찾는데 왜 위 식이 사용되는지 잘 와닿지 않으실 수 있습니다.
예를 들어보겠습니다. 다음과 같이 가중치 \(w\)에 대한 손실함수 \(E(w)\)가 있습니다. 앞서 말했다시피 우리의 목적은 손실함수의 최솟값을 가지는 \(w\)를 찾는 것입니다.

미분을 통해 이 함수의 그래디언트를 계산해 보면 \(2w - 6 \)가 됩니다. \(w = 10\) 부터 가중치 변경을 시작한다고 가정하고, 손실함수와 그래디언트 값을 계산하면 다음과 같습니다.
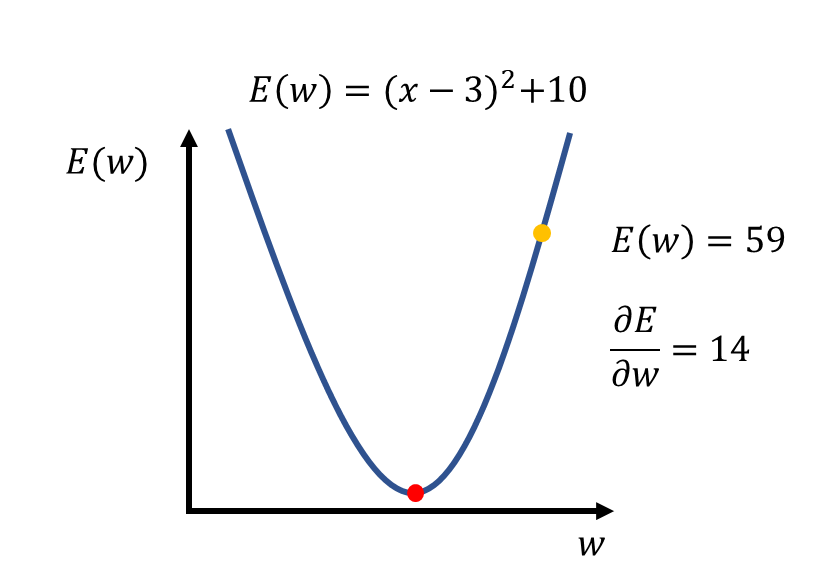
학습률을 0.2라고 가정하고 새로운 가중치를 계산하면 \((w+1) = 10-0.2*14\) 로 \(7.2\)가 됩니다. 그럼 변경된 가중치를 이용해 다시 한번 손실함수의 값을 계산해 볼까요?
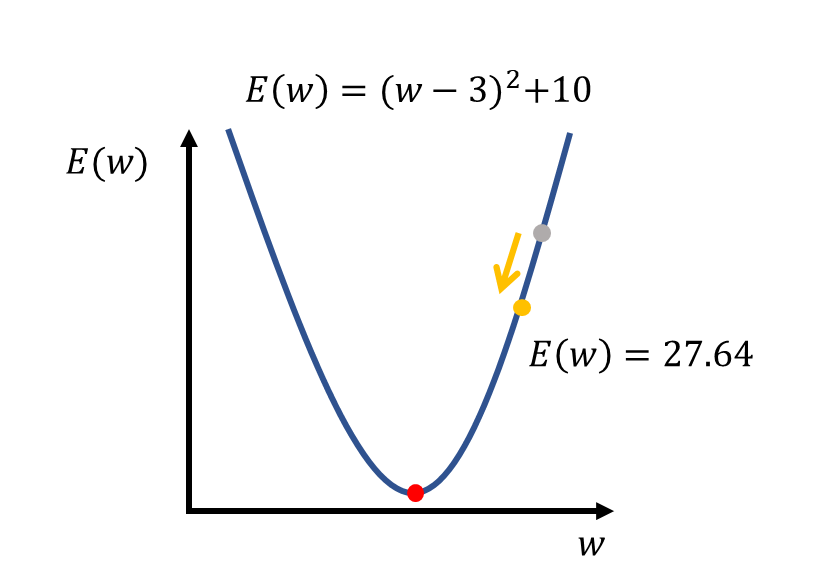
손실함수의 값이 줄어든 것을 확인할 수 있습니다. 정리하면, 그래디언트에 음수를 곱한 방향으로 마치 경사면을 따라 미끄러지듯 최솟값을 찾는 방법이 바로 경사하강법 입니다. 미분을 배우셨다면 아시다시피 그래디언트는 곧 기울기로 볼 수 있고, 최솟값에 가까워질수록 미분 값은 점점 작아지기 때문에 보통 임계값을 정해 해당 값보다 작아질 때까지 학습을 반복하도록 합니다.
역전파 알고리즘
이제 MLP의 꽃인 역전파 알고리즘에 대해 작성해 보도록 하겠습니다. 앞서 살펴본 예시의 경우 가중치가 하나이기 때문에 계산이 그리 복잡하지 않지만, 관여하는 가중치가 늘어날수록 그래디언트를 구하기 위한 계산이 중복되고 또 늘어나게 됩니다. 연구자들은 이를 효율적으로 실행하고자 역전파 알고리즘을 개발해냅니다.
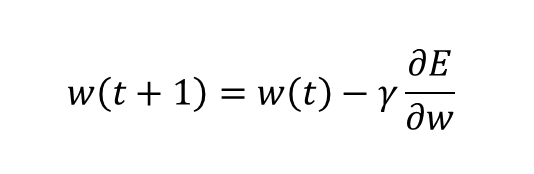
역전파 알고리즘이란 출력층에서 손실함수를 한 번만 계산한 후에 이를 신경망 반대로 전파하여 모든 위치에서 그래디언트를 계산할 수 있도록 하는 일종의 공식입니다. 체인 룰(chain rule, 연쇄 법칙)을 이용하여 정리하였으며 다음과 같습니다.
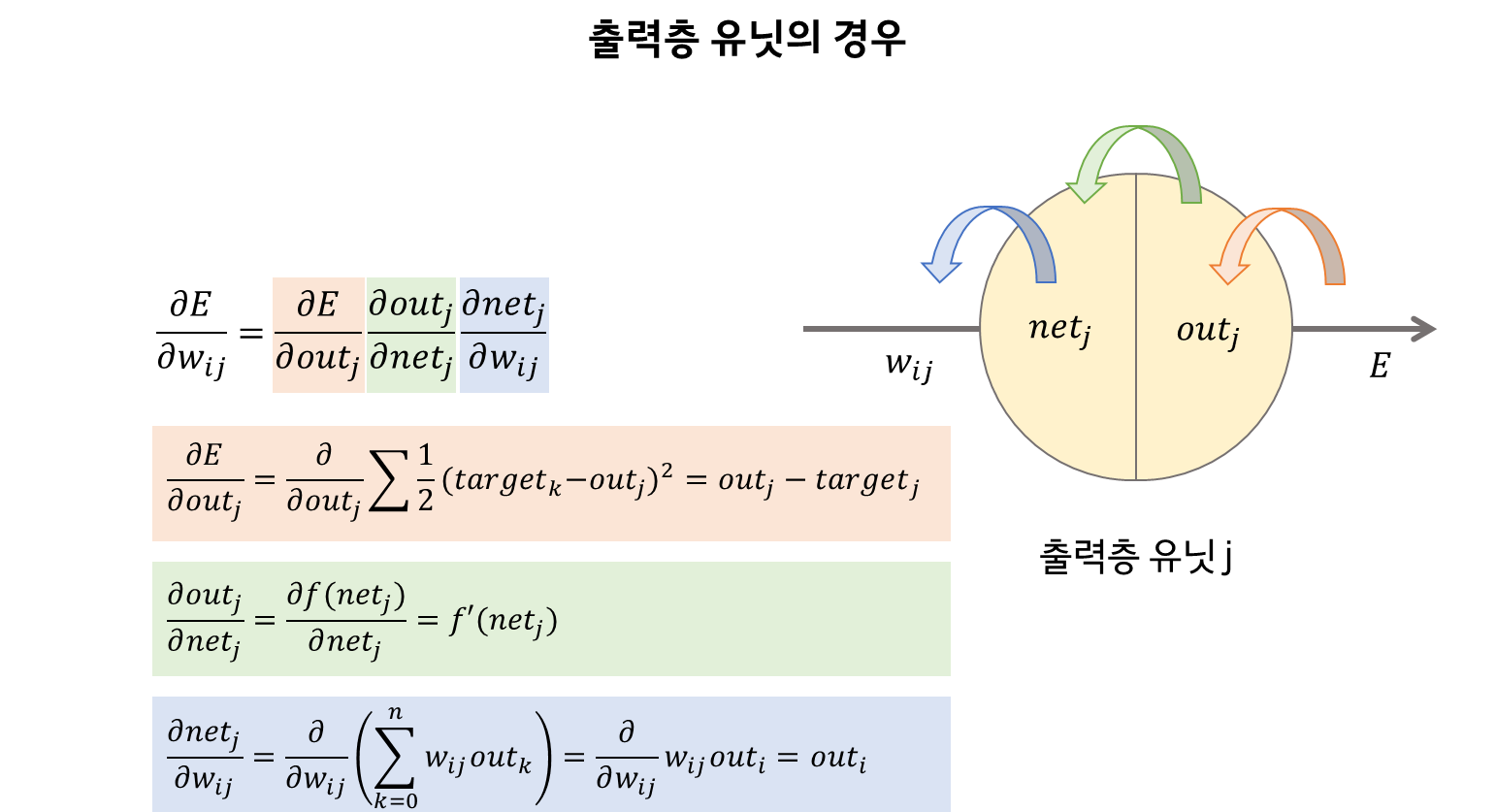
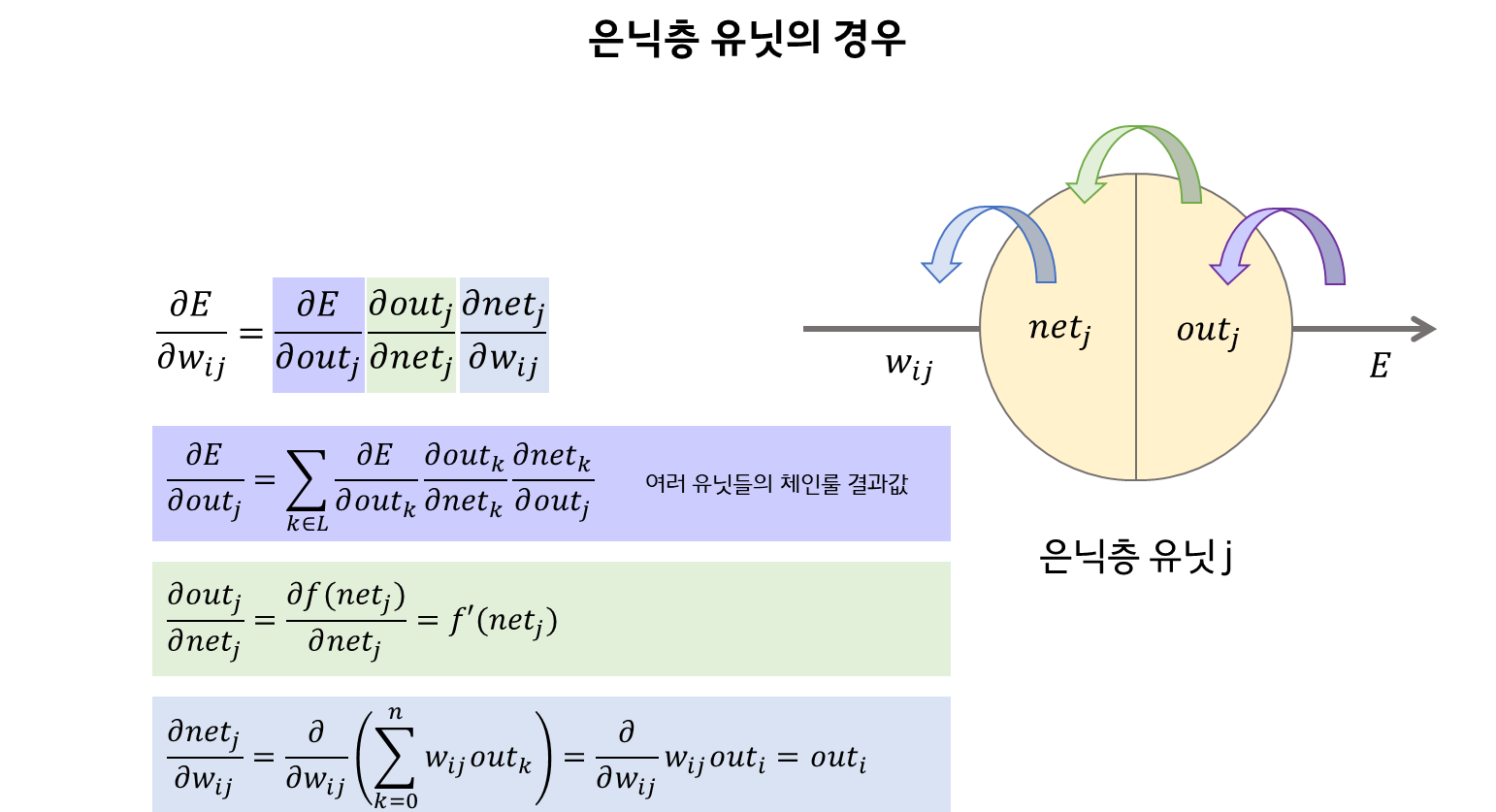
+ 연습문제
어떤 경우에는 구체적으로 계산을 해보는 것이 이해하는데 도움이 된다. 다음과 같이 2개의 입력과 하나의 출력을 가지는 MLP에서 원하는 출력 값이 0이라고 할 때, 각 뉴런의 출력 값과 오차를 계산해보자. 활성화 함수는 계산을 간단히 하기 위하여 ReLU함수라고 가정한다. 순방향 패스와 오차값만을 계산해보자.
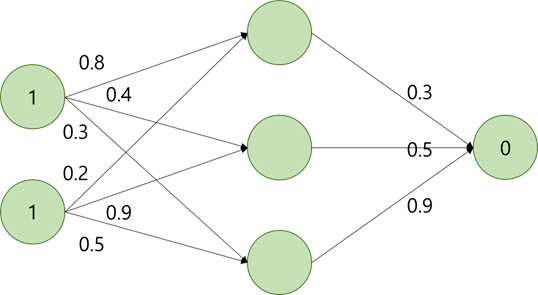
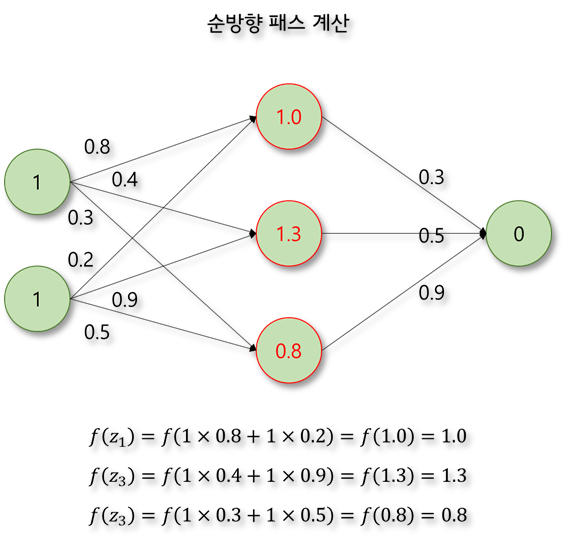
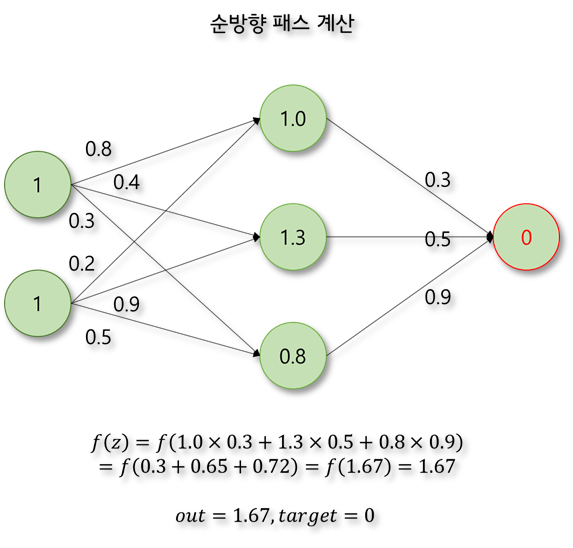

신경망에서 오차가 역전파되는 과정을 한 단계만 계산해보자. 활성화 함수는 계산을 간단히 하기 위하여 ReLU함수라고 가정한다.
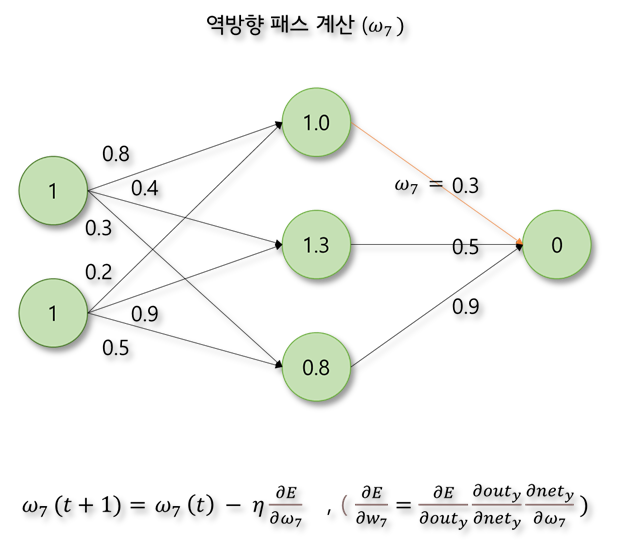
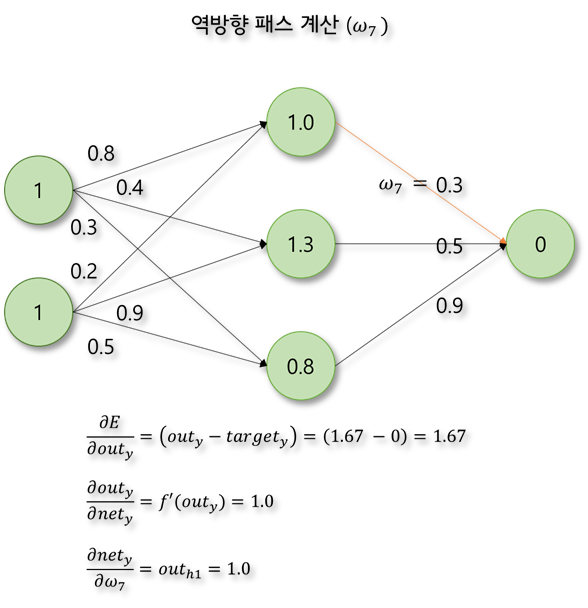
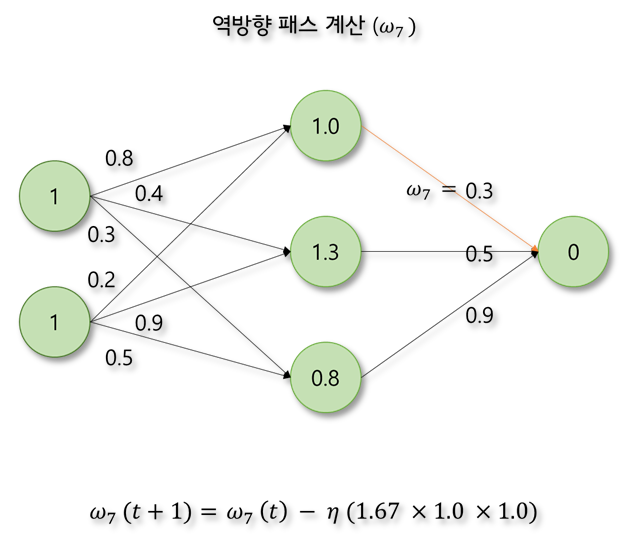
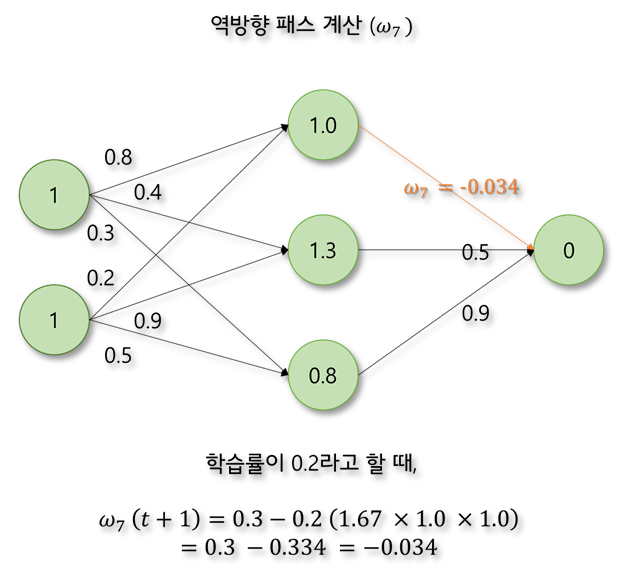
MLP와 역전파 알고리즘의 등장으로 신경망은 크게 관심을 받고 이는 현재까지 이어지고 있습니다. MLP를 기반으로 한 수많은 신경망들이 연구되었고 하드웨어의 발전으로 이전에는 어려웠던 다량의 데이터 처리와 계산이 가능해지면서 약인공지능으로서 뛰어난 성능을 보여주고 있습니다. 다음 글에서는 신경망 학습에 사용되는 요소들에 대해 좀 더 작성해 보겠습니다.
[인공지능] Numpy로 역방향전파 구현하기
[인공지능] 다층 퍼셉트론 (MLP)과 역전파 알고리즘 아래 글에 이어 작성된 글입니다. [인공지능] 인공신경망의 시작, 퍼셉트론 아래 글에 이어 작성된 글입니다. [인공지능] 머신러닝과 인공신경
munak.tistory.com
감사합니다.
공부한 내용을 복습/기록하기 위해 작성한 글이므로 내용에 오류가 있을 수 있습니다.
'인공지능' 카테고리의 다른 글
| [인공지능] 딥러닝과 Python 라이브러리 (0) | 2022.08.30 |
|---|---|
| [인공지능] 하이퍼 파라미터 (에포크/배치/학습률/옵티마이저/손실함수/활성화함수) (0) | 2022.08.09 |
| [인공지능] 인공신경망의 시작, 퍼셉트론 (0) | 2022.08.02 |
| [인공지능] 머신러닝과 인공신경망 (feat. 분류, 회귀) (0) | 2022.07.11 |
| [인공지능] 전문가 시스템과 지식 (0) | 2022.01.18 |
